
分析 畫出函數y=Z|x2-1,x+1,-x+1|的圖象,要使直線y=kx+$\frac{1}{2}$(k>0)與函數y=Z|x2-1,x+1,-x+1|的圖象有且只有2個交點,只需直線經過(2,3)和經過(2,$\frac{1}{2}$)之間.
解答 解: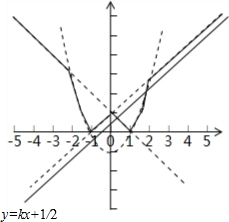 函數y=Z|x2-1,x+1,-x+1|的圖象如圖所示
函數y=Z|x2-1,x+1,-x+1|的圖象如圖所示
∵直線y=kx+$\frac{1}{2}$(k>0)與函數y=Z|x2-1,x+1,-x+1|的圖象有且只有2個交點,
當直線y=kx+$\frac{1}{2}$(k>0)經過點(2,3)時,則3=2k+$\frac{1}{2}$,
解得k=$\frac{5}{4}$,
當直線y=kx+$\frac{1}{2}$(k>0)經過點(-1,0)時,k=$\frac{1}{2}$,
當k=1時,平行于y=x+1,與函數y=Z|x2-1,x+1,-x+1|的圖象也有且僅有兩個交點;
∴直線y=kx+$\frac{1}{2}$(k>0)與函數y=Z|x2-1,x+1,-x+1|的圖象有且只有2個交點,則k的取值為$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
故答案為$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
點評 本題考查了一次函數的性質以及中位數的概念,數形結合思想的應用是解題的關鍵.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | (-a,5) | B. | (a,-5) | C. | (-a+2,5) | D. | (-a+4,5) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 這個球一定是黑球 | |
| B. | 摸到黑球、白球的可能性的大小一樣 | |
| C. | 這個球可能是白球 | |
| D. | 事先能確定摸到什么顏色的球 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=3(x+1)2+1 | B. | y=3(x+1)2-1 | C. | y=3(x-1)2+1 | D. | y=3(x-1)2-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
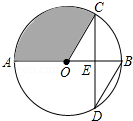 如圖,AB是⊙O的直徑,弦CD交AB于點E,且E為OB的中點,∠CDB=30°,CD=6$\sqrt{3}$,則陰影部分的面積為12π.
如圖,AB是⊙O的直徑,弦CD交AB于點E,且E為OB的中點,∠CDB=30°,CD=6$\sqrt{3}$,則陰影部分的面積為12π.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com