Question

4．已知△ABC中，∠ABC=m°，以AC為邊向形外作等邊△ACD，將△ADB繞D點逆時針旋轉60°至△CDE處，則∠BCE的度數為60°+m°或300°-m°．

Answer 1

分析 根據∠ABC=m°，分兩種情況進行討論：①當∠ABC=m°≤120°時，②當∠ABC=m°＞120°時，分別根據角的和差關系進行計算，即可得出∠BCE的度數．

解答 解：分兩種情況：
①如圖所示，當0°＜m°≤120°時，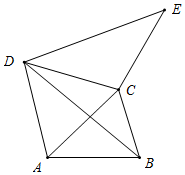

設∠BAC=α，∠ACB=β，則∠BAD=60°+α，α+β=180°-m°，
由旋轉可得，∠ECD=∠BAD=60°+α，
∴∠BCE=360°-∠ACB-∠ACD-∠ECD
=360°-β-60°-（60°+α）
=240°-（α+β）
=240°-（180°-m°）
=60°+m°；

②如圖所示，當120°＜m°＜180°時，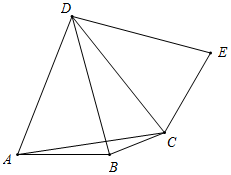

∠BAD=60°+α，α+β=180°-m°，
由旋轉可得，∠ECD=∠BAD=60°+α，
∴∠BCE=∠ACB+∠ACD+∠ECD
=β+60°+60°+α
=120°+（α+β）
=120°+180°-m°
=300°-m°．
綜上所述，∠BCE的度數為60°+m°或300°-m°．
故答案為：60°+m°或300°-m°．

點評 本題主要考查了旋轉的性質以及等邊三角形的性質，解決問題的關鍵是掌握：旋轉前、后的圖形全等，即對應角相等，對應邊相等．解題時注意：等邊三角形的三個角都是60°．