
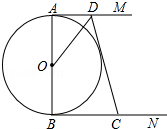
 如圖,AB是⊙O的直徑,AM、BN分別與⊙O相切于點A、B,CD交AM、BN于點D、C,DO平分∠ADC.
如圖,AB是⊙O的直徑,AM、BN分別與⊙O相切于點A、B,CD交AM、BN于點D、C,DO平分∠ADC.分析 (1)過O作OE⊥CD于點E,則∠OED=90°.依據切線的性質可知∠OAD=90°,接下來證明△OAD≌△OED,依據全等三角形的性質可知OA=OE,故此OE為⊙O的半徑,則CD是⊙O的切線;
(2)如圖2所示:過O作OE⊥CD于點E,過點D作DF⊥BC于點F,則DF=AB=x.由切線長定理可得:DE=DA,CE=CB,則CD=4+y,在Rt△DFC中依據勾股定理可得到(y+4)=x2+(y-4)2,從而可得到y與x的函數關系式.
解答 解:(1)過O作OE⊥CD于點E,則∠OED=90°.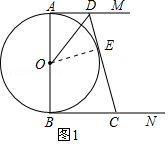
∵⊙O與AM相切于點A,
∴∠OAD=90°.
∵OD平分∠ADE,
∴∠ADO=∠EDO.
∵OD=OD,
∴△OAD≌△OED.
∴OE=OA.
∵OA是⊙O的半徑,
∴OE是⊙O的半徑.
∴CD是⊙O的切線.
(2)如圖2所示:過O作OE⊥CD于點E,過點D作DF⊥BC于點F,則DF=AB=x.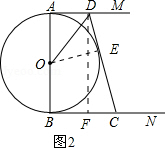
∵AD=4,BC=y,
∴CF=BC-AD=y-4.
由切線長定理可得:DE=DA,CE=CB,
∴CD=CE+ED
=BC+AD
=4+y
在Rt△DFC中,
∵CD2=DF2+FC2
∴(y+4)=x2+(y-4)2.
整理得:y=$\frac{1}{16}$x2,則y關于x的函數關系式為:y=$\frac{1}{16}$x2.
點評 本題主要考查的是切線的性質和判定,解答本題主要應用了切線的性質和判定定理、全等三角形的性質和判定,掌握本題的輔助線的作法是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
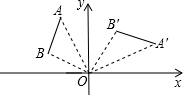 如圖,將線段AB繞點O順時針旋轉90°得到線段A′B′,那么A(-2,5)的對應點A′的坐標是( )
如圖,將線段AB繞點O順時針旋轉90°得到線段A′B′,那么A(-2,5)的對應點A′的坐標是( )| A. | (2,5) | B. | (5,2) | C. | (4,$\frac{5}{2}$) | D. | ($\frac{5}{2}$,4) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在直角坐標系xOy中,△ABC的三個頂點坐標分別為A(-4,1)、B(-1,1)、C(-4,3).
如圖,在直角坐標系xOy中,△ABC的三個頂點坐標分別為A(-4,1)、B(-1,1)、C(-4,3).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ①②③④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 將連續的奇數1,3,5,7,9,…排成如圖所示的數表,若陰影十字框上下左右移動,則陰影十字框中的五個數字之和可以是( )
將連續的奇數1,3,5,7,9,…排成如圖所示的數表,若陰影十字框上下左右移動,則陰影十字框中的五個數字之和可以是( )| A. | 2025 | B. | 2020 | C. | 2017 | D. | 2018 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 第一套 | 第二套 | |
| 椅子高度xcm | 40.0 | 38.0 |
| 課桌高度ycm | 75.0 | 71.8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com