
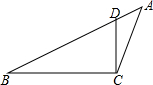
 如圖,在△ABC中,點D在AB上,在下列四個條件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能滿足△ADC與△ACB相似的條件是( )
如圖,在△ABC中,點D在AB上,在下列四個條件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能滿足△ADC與△ACB相似的條件是( )| A. | ①、②、③ | B. | ①、③、④ | C. | ②、③、④ | D. | ①、②、④ |
分析 由∠A是公共角,根據有兩組角對應相等的兩個三角形相似與兩組對應邊的比相等且夾角對應相等的兩個三角形相似,判定△ABC與△ACD相似,即可得出結果.
解答 解:∵∠A是公共角,
∴當∠ACD=∠B時,△ADC∽△ACB(有兩組角對應相等的兩個三角形相似);
當∠ADC=∠ACB時,△ADC∽△ACB(有兩組角對應相等的兩個三角形相似);
當AC2=AD•AB時,即$\frac{AC}{AB}=\frac{AD}{AC}$,△ADC∽△ACB(兩組對應邊的比相等且夾角對應相等的兩個三角形相似).
當AB•CD=AD•CB,即$\frac{CD}{AD}=\frac{CB}{AB}$時,∠A不是夾角,則不能判定△ADC與△ACB相似;
∴能夠判定△ABC與△ACD相似的條件是:①②③.
故選A.
點評 此題考查了相似三角形的判定.此題難度不大,熟記相似三角形的判定方法是解決問題的關鍵.


科目:初中數學 來源: 題型:選擇題
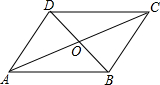 如圖,?ABCD對角線AC與BD相交于點O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列選項中,與向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如圖,?ABCD對角線AC與BD相交于點O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列選項中,與向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )| A. | $\overrightarrow{OA}$ | B. | $\overrightarrow{OB}$ | C. | $\overrightarrow{OC}$ | D. | $\overrightarrow{OD}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知:矩形OABC的頂點A,C分別在x,y軸的正半軸上,O為平面直角坐標系的原點;直線y=x+1分別交x,y軸及矩形OABC的BC邊于E,M,F,且△EOM≌△FCM;過點F的雙曲線y=$\frac{k}{x}$(x>0)與AB交于點N.
如圖,已知:矩形OABC的頂點A,C分別在x,y軸的正半軸上,O為平面直角坐標系的原點;直線y=x+1分別交x,y軸及矩形OABC的BC邊于E,M,F,且△EOM≌△FCM;過點F的雙曲線y=$\frac{k}{x}$(x>0)與AB交于點N.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com