
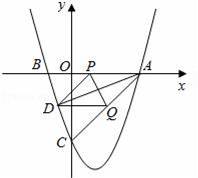
如圖,二次函數y=
 x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),與y軸交于點C.若點P,Q同時從A點出發,都以每秒1個單位長度的速度分別沿AB,AC邊運動,其中一點到達端點時,另一點也隨之停止運動.
x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),與y軸交于點C.若點P,Q同時從A點出發,都以每秒1個單位長度的速度分別沿AB,AC邊運動,其中一點到達端點時,另一點也隨之停止運動.
(1)求該二次函數的解析式及點C的坐標;
(2)當點P運動到B點時,點Q停止運動,這時,在x軸上是否存在點E,使得以A,E,Q為頂點的三角形為等腰三角形?若存在,請求出E點坐標;若不存在,請說明理由.
(3)當P,Q運動到t秒時,△APQ沿PQ翻折,點A恰好落在拋物線上D點處,請判定此時四邊形APDQ的形狀,并求出D點坐標.


【考點】二次函數綜合題.
【專題】代數幾何綜合題;壓軸題.
【分析】(1)將A,B點坐標代入函數y=
 x2+bx+c中,求得b、c,進而可求解析式及C坐標.
x2+bx+c中,求得b、c,進而可求解析式及C坐標.
(2)等腰三角形有三種情況,AE=EQ,AQ=EQ,AE=AQ.借助垂直平分線,畫圓易得E大致位置,設邊長為x,表示其他邊后利用勾股定理易得E坐標.
(3)注意到P,Q運動速度相同,則△APQ運動時都為等腰三角形,又由A、D對稱,則AP=DP,AQ=DQ,易得四邊形四邊都相等,即菱形.利用菱形對邊平行且相等等性質可用t表示D點坐標,又D在E函數上,所以代入即可求t,進而D可表示.
【解答】方法(1):
解:(1)∵二次函數y=
 x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),
x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),
∴
 ,
,
解得
 ,
,
∴y=
 x2﹣
x2﹣
 x﹣4.
x﹣4.
∴C(0,﹣4).
(2)存在.
如圖1,過點Q作QD⊥OA于D,此時QD∥OC,


∵A(3,0),B(﹣1,0),C(0,﹣4),O(0,0),
∴AB=4,OA=3,OC=4,
∴AC=
 =5,
=5,
∵當點P運動到B點時,點Q停止運動,AB=4,
∴AQ=4.
∵QD∥OC,
∴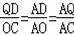
 ,
,
∴
 ,
,
∴QD=
 ,AD=
,AD=
 .
.
①作AQ的垂直平分線,交AO于E,此時AE=EQ,即△AEQ為等腰三角形,


設AE=x,則EQ=x,DE=AD﹣AE=|
 ﹣x|,
﹣x|,
∴在Rt△EDQ中,(
 ﹣x)2+(
﹣x)2+(
 )2=x2,解得 x=
)2=x2,解得 x=
 ,
,
∴OA﹣AE=3﹣
 =﹣
=﹣
 ,
,
∴E(﹣
 ,0),
,0),
說明點E在x軸的負半軸上;
②以Q為圓心,AQ長半徑畫圓,交x軸于E,此時QE=QA=4,
∵ED=AD=
 ,
,
∴AE=
 ,
,
∴OA﹣AE=3﹣
 =﹣
=﹣
 ,
,
∴E(﹣
 ,0).
,0).
③當AE=AQ=4時,
1.當E在A點左邊時,
∵OA﹣AE=3﹣4=﹣1,
∴E(﹣1,0).
2.當E在A點右邊時,
∵OA+AE=3+4=7,
∴E(7,0).
綜上所述,存在滿足條件的點E,點E的坐標為(﹣
 ,0)或(﹣
,0)或(﹣
 ,0)或(﹣1,0)或(7,0).
,0)或(﹣1,0)或(7,0).
(3)四邊形APDQ為菱形,D點坐標為(﹣
 ,﹣
,﹣
 ).理由如下:
).理由如下:
如圖2,D點關于PQ與A點對稱,過點Q作,FQ⊥AP于F,


∵AP=AQ=t,AP=DP,AQ=DQ,
∴AP=AQ=QD=DP,
∴四邊形AQDP為菱形,
∵FQ∥OC,
∴
 ,
,
∴
 ,
,
∴AF=
 ,FQ=
,FQ=
 ,
,
∴Q(3﹣
 ,﹣
,﹣
 ),
),
∵DQ=AP=t,
∴D(3﹣
 ﹣t,﹣
﹣t,﹣
 ),
),
∵D在二次函數y=
 x2﹣
x2﹣
 x﹣4上,
x﹣4上,
∴﹣
 =
=
 (3﹣
(3﹣
 t)2﹣
t)2﹣
 (3﹣
(3﹣
 t)﹣4,
t)﹣4,
∴t=
 ,或t=0(與A重合,舍去),
,或t=0(與A重合,舍去),
∴D(﹣
 ,﹣
,﹣
 ).
).
方法二:
(1)略.
(2)∵點P、Q同時從A點出發,都已每秒1個單位長度的速度分別沿AB,AC運動.過點Q作x軸垂線,垂足為H.
∵A(3,0),C(0,4),
∴lAC:y=
 x﹣4,
x﹣4,
∵點P運動到B點時,點Q停止運動,
∴AP=AQ=4,
∴QH=
 ,Qy=﹣
,Qy=﹣
 ,
,
代入LAC:y=
 x﹣4得,Qx=
x﹣4得,Qx=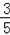
 ,則Q(
,則Q(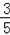
 ,﹣
,﹣
 ),
),
∵點E在x軸上,
∴設E(a,0),
∵A(3,0),Q(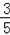
 ,﹣
,﹣
 ),△AEQ為等腰三角形,
),△AEQ為等腰三角形,
∴AE=EQ,AE=AQ,EQ=AQ,
∴(a﹣3)2=(a﹣
 )2+(0+
)2+(0+
 )2,∴a=﹣
)2,∴a=﹣
 ,
,
(a﹣3)2=(3﹣
 )2+(0+
)2+(0+
 )2,∴a1=7,a2=﹣1,
)2,∴a1=7,a2=﹣1,
(a﹣
 )2+(0+
)2+(0+
 )2=(3﹣
)2=(3﹣
 )2+(0+
)2+(0+
 )2,∴a1=﹣
)2,∴a1=﹣
 ,a2=3(舍)
,a2=3(舍)
∴點E的坐標為(﹣
 ,0)或(﹣
,0)或(﹣
 ,0)或(﹣1,0)或(7,0).
,0)或(﹣1,0)或(7,0).
(3)∵P,Q運動到t秒,
∴設P(3﹣t,0),Q(3﹣
 t,﹣
t,﹣
 t),
t),
∴KPQ=
 ,KPQ=﹣2,
,KPQ=﹣2,
∵AD⊥PQ,
∴KPQ•KAD=﹣1,
∴KAD=
 ,
,
∵A(3,0),
∴lAD:y=
 x﹣
x﹣
 ,
,
∵y=
 ,
,
∴x1=3(舍),x2=﹣
 ,
,
∴D(﹣
 ,﹣
,﹣
 ),
),
∵DY=QY,即﹣
 t=﹣
t=﹣
 ,t=
,t=
 ,DQ∥AP,DQ=AQ=AP,此時四邊形APDQ的形狀為菱形.
,DQ∥AP,DQ=AQ=AP,此時四邊形APDQ的形狀為菱形.



【點評】本題考查了二次函數性質、利用勾股定理解直角三角形及菱形等知識,總體來說題意復雜但解答內容都很基礎,是一道值得練習的題目.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數學 來源: 題型:
在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC邊于點E,則線段BE,EC的長度分別為( )


A.2和3 B.3和2 C.4和1 D.1和4
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,三個正方形圍成一個直角三角形,64,400分別為所在正方形的面積,則圖中字母所代表的正方形面積是( )


A.400+64 B.
 C.400﹣64 D.4002﹣642
C.400﹣64 D.4002﹣642
查看答案和解析>>
科目:初中數學 來源: 題型:
遵義市某中學為了搞好“創建全國文明城市”的宣傳活動,對本校部分學生(隨機抽查)進行了一次相關知識了解程度的調查測試(成績分為A、B、C、D、E五個組,x表示測試成績).通過對測試成績的分析,得到如圖所示的兩幅不完整的統計圖.請你根據圖中提供的信息解答以下問題:


(1)參加調查測試的學生為 人;
(2)將條形統計圖補充完整;
(3)本次調查測試成績中的中位數落在 組內;
(4)若測試成績在80分以上(含80分)為優秀,該中學共有學生2600人,請你根據樣本數據估計全校學生測試成績為優秀的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
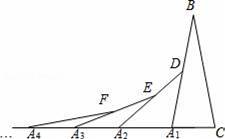
如圖,在第1個△A1BC中,∠B=20°,A1B=CB;在邊A1B上任取一點D,延長CA1到A2,使A1A2=A1D,得到第2個△A1A2D;在邊A2D上任取一點E,延長A1A2到A3,使A2A3=A2E,得到第3個△A2A3E,…按此做法繼續下去,則第5個三角形中以A5為頂點的內角度數是 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com