
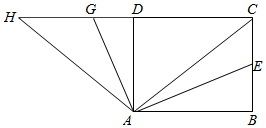
分析 設∠BAE=∠GAH=α,∠DAG=β,由四邊形ABCD是矩形,得到∠B=90°,根據勾股定理得到AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\frac{\sqrt{73}}{2}$,由三角函數的定義得到sinα,cosα,sin(α+β),cos(α+β)=$\frac{AD}{AH}$,根據兩角和和兩角差的正余弦公式求得cosβ,sinβ,于是得到tanβ,即可得到結論.
解答  解:設∠BAE=∠GAH=α,∠DAG=β,
解:設∠BAE=∠GAH=α,∠DAG=β,
∵四邊形ABCD是矩形,
∴∠B=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\frac{\sqrt{73}}{2}$,
∴sinα=$\frac{3}{2\sqrt{73}}$,cosα=$\frac{4}{\sqrt{73}}$,
∴sin(α+β)=$\frac{HD}{AH}=\frac{4}{5}$,cos(α+β)=$\frac{AD}{AH}$=$\frac{3}{5}$,
∴cosβ=cos(α+β-α)=cos(α+β)•cosα+sin(α+β)•sinβ=$\frac{3}{5}$×$\frac{4}{\sqrt{73}}$+$\frac{4}{5}$•$\frac{3}{2\sqrt{73}}$=$\frac{18}{5\sqrt{73}}$,
sinβ=sin(α+β-α)=sin(α+β)•cosα-cos(α+β)•sinα=$\frac{4}{5}$×$\frac{4}{\sqrt{73}}$-$\frac{3}{5}$×$\frac{3}{2\sqrt{73}}$=$\frac{23}{10\sqrt{73}}$,
∴tanβ=$\frac{sinβ}{cosβ}$=$\frac{23}{36}$=$\frac{GD}{AD}$,
∴DG=AD•tanβ=3×$\frac{23}{36}$=$\frac{23}{12}$,
∴CG=4+$\frac{23}{12}$=$\frac{71}{12}$.
故答案為:$\frac{71}{12}$.
點評 本題考查了旋轉的性質,勾股定理,矩形的性質,三角函數,熟練掌握旋轉的性質是解題的關鍵.


科目:初中數學 來源: 題型:填空題
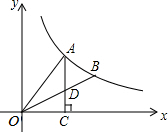 如圖,A.B是雙曲線y=$\frac{k}{x}$上的兩點,過A點作AC⊥x軸,交OB于D點,垂足為C.若△ADO的面積為1,D為OB的中點,則k的值為$\frac{8}{3}$.
如圖,A.B是雙曲線y=$\frac{k}{x}$上的兩點,過A點作AC⊥x軸,交OB于D點,垂足為C.若△ADO的面積為1,D為OB的中點,則k的值為$\frac{8}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
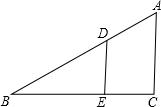 如圖,D為直角三角形ABC斜邊上一點,DE⊥BC于E點,BE=AC,若BD=$\frac{1}{2}$厘米,DE+BC=1厘米,試求∠B的大小.
如圖,D為直角三角形ABC斜邊上一點,DE⊥BC于E點,BE=AC,若BD=$\frac{1}{2}$厘米,DE+BC=1厘米,試求∠B的大小.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
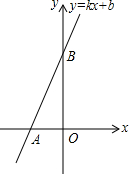 如圖,直線y=kx+b交坐標軸于A(-2,0),B(0,4)兩點,則不等式kx+b<0的解集為( )
如圖,直線y=kx+b交坐標軸于A(-2,0),B(0,4)兩點,則不等式kx+b<0的解集為( )| A. | x<-2 | B. | x>-2 | C. | x>2 | D. | x<2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com