
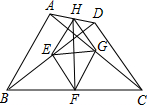
 如圖,四邊形ABCD,AD與BC不平行,AB=CD.AC,BD為四邊形ABCD的對角線.E,F,G,H分別是BD,BC,AC,AD的中點.
如圖,四邊形ABCD,AD與BC不平行,AB=CD.AC,BD為四邊形ABCD的對角線.E,F,G,H分別是BD,BC,AC,AD的中點.| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 先根據三角形中位線定理,得出EF=FG=GH=HE,進而得到四邊形EFGH是菱形,據此可判斷結論是否正確,最后取AB的中點P,連接PE,PG,根據三角形三邊關系以及三角形中位線定理,即可得出EG>$\frac{1}{2}$BC-$\frac{1}{2}$AD,即EG>$\frac{1}{2}$(BC-AD).
解答  解:∵E,F分別是BD,BC的中點,
解:∵E,F分別是BD,BC的中點,
∴EF是△BCD的中位線,
∴EF=$\frac{1}{2}$CD,
同理可得,GH=$\frac{1}{2}$CD,FG=$\frac{1}{2}$AB,EH=$\frac{1}{2}$AB,
又∵AB=CD,
∴EF=FG=GH=HE,
∴四邊形EFGH是菱形,故⑤正確,②錯誤,
∴EG⊥FH,HF平分∠EHG,故①、③正確,
如圖所示,取AB的中點P,連接PE,PG,
∵E是BD的中點,G是AC的中點,
∴PE是△ABD的中位線,PG是△ABC的中位線,
∴PE=$\frac{1}{2}$AD,PG=$\frac{1}{2}$BC,PE∥AD,PG∥BC,
∵AD與BC不平行,
∴PE與PG不平行,
∴△PEG中,EG>PG-PE,
∴EG>$\frac{1}{2}$BC-$\frac{1}{2}$AD,即EG>$\frac{1}{2}$(BC-AD),故④錯誤.
綜上所述,正確的有①③⑤.
故選:C.
點評 本題主要考查了中點四邊形,三角形三邊關系以及三角形中位線定理的運用,解題時注意:三角形的中位線平行于第三邊,并且等于第三邊的一半.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:初中數學 來源: 題型:選擇題
 小明在做選擇題“如圖,四邊形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,則BC的長為多少”時遇到了困難.小明通過度量發現,試題給出的圖形中,AD=3cm,BC=1.05cm,且各角度符合條件,因此小明猜想下列選項中最有可能正確的是( )
小明在做選擇題“如圖,四邊形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,則BC的長為多少”時遇到了困難.小明通過度量發現,試題給出的圖形中,AD=3cm,BC=1.05cm,且各角度符合條件,因此小明猜想下列選項中最有可能正確的是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
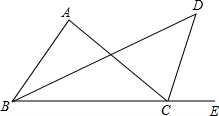 如圖,△ABC中,∠ABC的平分線與∠ACE的平分線相交于點D.
如圖,△ABC中,∠ABC的平分線與∠ACE的平分線相交于點D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,一個尋寶游戲的尋寶結構是等邊三角形ABC及中心O,通道是AB,BC,CA,OA,OB,OC組成.為記錄尋寶者的進行路線,將定位儀放置在BC的中點M處,尋寶者的行進路線為B→O→C,若尋寶者勻速行進,設尋寶者行進的時間為x,尋寶者與定位儀之間的距離為y,則y與x的函數關系的圖象大致可能為( )
如圖,一個尋寶游戲的尋寶結構是等邊三角形ABC及中心O,通道是AB,BC,CA,OA,OB,OC組成.為記錄尋寶者的進行路線,將定位儀放置在BC的中點M處,尋寶者的行進路線為B→O→C,若尋寶者勻速行進,設尋寶者行進的時間為x,尋寶者與定位儀之間的距離為y,則y與x的函數關系的圖象大致可能為( )| A. | 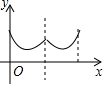 | B. | 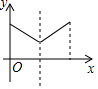 | C. | 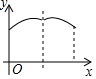 | D. | 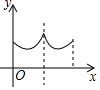 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
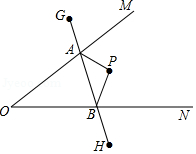 如圖,∠MON內有一點P,P點關于OM的軸對稱點是G,P點關于ON的軸對稱點是H,GH分別交OM、ON于A、B點.若GH的長為14,則△PAB的周長為14.
如圖,∠MON內有一點P,P點關于OM的軸對稱點是G,P點關于ON的軸對稱點是H,GH分別交OM、ON于A、B點.若GH的長為14,則△PAB的周長為14.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 平均數 | B. | 中位數 | C. | 眾數 | D. | 以上都不對 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com