
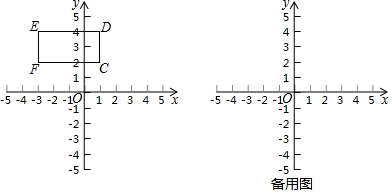
分析 (1)把拋物線解析式化為頂點式可求得其頂點坐標;
(2)由拋物線的對稱性可知當開口向上時,離對稱軸越近其函數值則越小,則可求得答案;
(3)由于拋物線的頂點確定,且開口向上,所以當拋物線開口越大時a的值越小,當拋物線開口越小時a的值越大,可知當拋物線過C時a有最小值,當拋物線過F時a有最大值,則可求得a的取值范圍.
解答 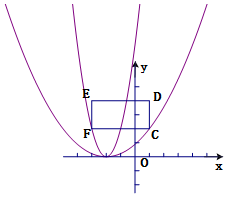 解:
解:
(1)∵y=a ( x 2+4x+4 )=a ( x+2 ) 2,
∴拋物線的頂點坐標為(-2,0);
(2)∵a>0,且對稱軸為直線x=-2,
∴當函數圖象上的點離對稱軸越近時其函數值越小,
∵-4<m≤-3,0<n≤1,
∴A點離對稱軸x=-2近,
∴y 1<y 2,
故答案為:<;
(3)∵y=a ( x+2 ) 2開口向上,且頂點為(-2,0),
∴當開口越大時a的值越小,當開口越小時a的值越大,
∴當拋物線過點C時a有最小值,當拋物線過點F時a有最大值
代入點C(1,2),得a=$\frac{2}{9}$,
代入點F(-3,2),得a=2,
∴$\frac{2}{9}$<a<2.
點評 本題為二次函數的綜合應用,涉及二次函數的性質、二次函數的開口大小、二次函數的比較大小及數形結合思想等知識.在(1)中把二次函數解析式化為頂點式是解題的關鍵,在(2)中掌握拋物線上的點離對稱軸的距離的遠近與函數值的大小關系是解題的關鍵,在(3)中掌握拋物線的開口大小與二次項系數的關系是解題的關鍵.本題考查知識點不多,但綜合性很強,難度適中.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:選擇題
| 1 | 2 | 3 | 4 | … |
| 2 | 4 | 6 | 8 | … |
| 3 | 6 | 9 | 12 | … |
| 4 | 8 | 12 | 16 | … |
| … | … | … | … | … |
| 10 | |
| a | |
| 21 |
| A. | 16 | B. | 18 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | |a+b|的值一定是正數 | B. | a2+1的值一定是正數 | ||
| C. | 當a<b時,a2<b2 | D. | 當a>b時,|a|>|b| |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
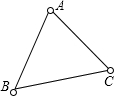 如圖,兔子的三個洞口A、B、C構成△ABC,獵狗想捕捉兔子,必須到三個洞口的距離都相等,則獵狗應蹲守在( )
如圖,兔子的三個洞口A、B、C構成△ABC,獵狗想捕捉兔子,必須到三個洞口的距離都相等,則獵狗應蹲守在( )| A. | 三條邊的垂直平分線的交點 | B. | 三個角的角平分線的交點 | ||
| C. | 三角形三條高的交點 | D. | 三角形三條中線的交點 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,兩棵大樹間相距13m,小華從點B沿BC走向點C,行走一段時間后他到達點E,此時他仰望兩棵大樹的頂點A和D,兩條視線的夾角正好為90°,且EA=ED.已知大樹AB的高為5m,小華行走的速度為lm/s,小華走的時間是( )
如圖,兩棵大樹間相距13m,小華從點B沿BC走向點C,行走一段時間后他到達點E,此時他仰望兩棵大樹的頂點A和D,兩條視線的夾角正好為90°,且EA=ED.已知大樹AB的高為5m,小華行走的速度為lm/s,小華走的時間是( )| A. | 13 | B. | 8 | C. | 6 | D. | 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com