Question

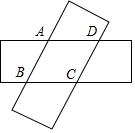
16．如圖，由兩個長為9，寬為3的全等矩形疊合而得到四邊形ABCD，則四邊形ABCD面積的最大值是（　　）

• A． 15
• B． 16
• C． 19
• D． 20

Answer 1

分析 首先根據圖1，證明四邊形ABCD是菱形；然后判斷出菱形的一條對角線為矩形的對角線時，四邊形ABCD的面積最大，設AB=BC=x，則BE=9-x，利用勾股定理求出x的值，即可求出四邊形ABCD面積的最大值是多少．

解答 解：如圖1，作AE⊥BC于E，AF⊥CD于F，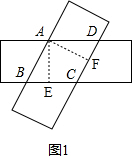
，
∵AD∥BC，AB∥CD，
∴四邊形ABCD是平行四邊形，
∵兩個矩形的寬都是3，
∴AE=AF=3，
∵S_{四邊形ABCD}=AE•BC=AF•CD，
∴BC=CD，
∴平行四邊形ABCD是菱形．

如圖2，
，
設AB=BC=x，則BE=9-x，
∵BC²=BE²+CE²，
∴x²=（9-x）²+3²，
解得x=5，
∴四邊形ABCD面積的最大值是：
5×3=15．
故選：A．

點評 此題主要考查了菱形的判定和性質，矩形的性質和應用，以及勾股定理的應用，要熟練掌握．