
 如圖,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直線CM⊥BC,動點D從點C開始以每秒2cm的速度運動到B點,動點E也同時從點C開始沿射線CM方向以每秒1cm的速度運動.
如圖,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直線CM⊥BC,動點D從點C開始以每秒2cm的速度運動到B點,動點E也同時從點C開始沿射線CM方向以每秒1cm的速度運動.分析 (1)設動點D運動t秒時,△ABD≌△ACE,先根據等腰直角三角形得:∠ACE=∠B,再加上AB=AC,所以只要滿足BD=CE,△ABD≌△ACE,列式可求得t的值;
(2)作高線AF,根據等腰直角三角形三線合一可知:AF是斜邊的中線,再由直角三角形斜邊的中線等于斜邊的一半得:AF=3,代入面積公式可求出代數式;
(3)作高線AG,先證明四邊形AFCG是矩形,求出AG=3,由△ABD與△ACE的面積比為3:1列式可得出結論.
解答 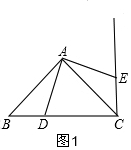 解:(1)如圖1,設動點D運動t秒時,△ABD≌△ACE,
解:(1)如圖1,設動點D運動t秒時,△ABD≌△ACE,
由題意得:CD=2t,CE=t,則BD=6-2t,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵CM⊥BC,
∴∠BCM=90°,
∴∠ACE=90°-45°=45°,
∴∠ACE=∠B,
∴當BD=CE時,△ABD≌△ACE,
即6-2t=t,
t=2,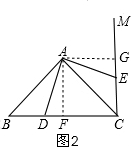
答:動點D運動2秒時,△ABD≌△ACE;
(2)如圖2,過A作AF⊥BC于F,
∵AB=AC,∠BAC=90°,
∴AF是斜邊的中線,
∴AF=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
由題意得:CD=2x,則BD=6-2x,
∴S=S△ABD=$\frac{1}{2}$BD•AF=$\frac{1}{2}$(6-2x)×3=-3x+9;
(3)設動點D運動x秒時,△ABD與△ACE的面積比為3:1,
如圖2,再過A作AG⊥CM于G,
∵∠AFC=∠BCM=∠AGC=90°,
∴四邊形AFCG是矩形,
∴AG=CF=$\frac{1}{2}$BC=3,
∵△ABD與△ACE的面積比為3:1,
∴$\frac{{S}_{△ABD}}{{S}_{△ACE}}$=$\frac{\frac{1}{2}BD•AF}{\frac{1}{2}CE•AG}$=$\frac{3}{1}$,
∴$\frac{BD}{CE}$=3,
∴BD=3CE,
即6-2x=3x,
5x=6,
x=$\frac{6}{5}$,
∴動點D運動$\frac{6}{5}$秒時,△ABD與△ACE的面積比為3:1.
點評 本題考查了等腰直角三角形、全等三角形的性質和判定以及動點問題,熟練掌握全等三角形的判定方法是關鍵,在動點問題中,明確路程=時間×速度,根據時間準確表示動點D和E的路程BD、CE的代數式,根據題中的等量關系列等式即可.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:初中數學 來源: 題型:解答題
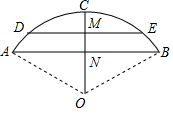 一跨河橋,橋拱是圓弧形,跨度(AB)為12米,拱高(CN)為2米,
一跨河橋,橋拱是圓弧形,跨度(AB)為12米,拱高(CN)為2米,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
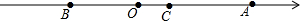 如圖,在數軸上原點O表示的數是0,B點表示的數是m,A表示的數是n,且(m+4)2+|n-8|=0.
如圖,在數軸上原點O表示的數是0,B點表示的數是m,A表示的數是n,且(m+4)2+|n-8|=0.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com