
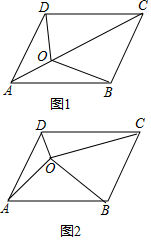
 我們知道平行四邊形的兩條對角線把平行四邊形分成了四個面積相等的小三角形.
我們知道平行四邊形的兩條對角線把平行四邊形分成了四個面積相等的小三角形.分析 (1)首先連接BD,交AC于點E,由四邊形ABCD是平行四邊形,可得BE=DE,然后由三角形中線的性質,證得S△ABE=S△ADE,S△OBE=S△ODE,S△BCE=S△DCE,繼而求得答案.
(2)過O作EF⊥AD,交AD于E,交CD于F,由三角形面積公式得出S△AOD=$\frac{1}{2}$AD•OE,S△BOC=$\frac{1}{2}$BC•OF,由平行四邊形的性質得出∴S△AOD+S△BOC=$\frac{1}{2}$BC•EF=$\frac{1}{2}$四邊形ABCD的面積,同理:S△AOB+S△COD=$\frac{1}{2}$平行四邊形ABCD的面積,即可得出結論.
解答 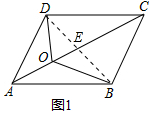 解:(1)不成立.S△OAB=S△OAD,S△BOC=S△DOC.理由如下:
解:(1)不成立.S△OAB=S△OAD,S△BOC=S△DOC.理由如下:
連接BD,交AC于點E,
∵四邊形ABCD是平行四邊形,
∴BE=DE,
∴S△ABE=S△ADE,S△OBE=S△ODE,S△BCE=S△DCE,
∴S△OAB=S△OAD,S△BOC=S△DOC.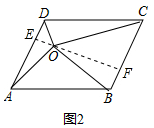
(2)S△AOD+S△BOC=S△AOB+S△COD.理由如下:
過O作EF⊥AD,交AD于E,交CD于F,如圖2所示:
則S△AOD=$\frac{1}{2}$AD•OE,S△BOC=$\frac{1}{2}$BC•OF,
∴S△AOD+S△BOC=$\frac{1}{2}$BC•(OE+OF)=$\frac{1}{2}$BC•EF=$\frac{1}{2}$四邊形ABCD的面積,
同理:S△AOB+S△COD=$\frac{1}{2}$平行四邊形ABCD的面積,
∴S△AOD+S△BOC=S△AOB+S△COD.
點評 此題考查了平行四邊形的性質以及三角形面積公式.熟練掌握平行四邊形的性質和三角形面積公式,注意掌握輔助線的作法,注意掌握數形結合思想的應用.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,直線l1:y=x+1與直線l2:y=mx+n相交于點P(1,b).
如圖,直線l1:y=x+1與直線l2:y=mx+n相交于點P(1,b).查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
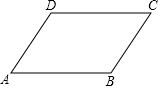 如圖,在?ABCD中,下列等式成立的是( )
如圖,在?ABCD中,下列等式成立的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$+$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
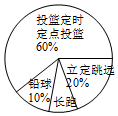 某班同學響應“陽光體育運動”號召,利用課外活動積極參加體育鍛煉,每位同學從長跑、鉛球、立定跳遠、籃球定時定點投籃中任選一項進行了訓練,訓練后都進行了測訓練后籃球定點投籃測試進行球賽進球統計表
某班同學響應“陽光體育運動”號召,利用課外活動積極參加體育鍛煉,每位同學從長跑、鉛球、立定跳遠、籃球定時定點投籃中任選一項進行了訓練,訓練后都進行了測訓練后籃球定點投籃測試進行球賽進球統計表| 進球數(個) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人數 | 2 | 1 | 4 | 7 | 8 | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com