
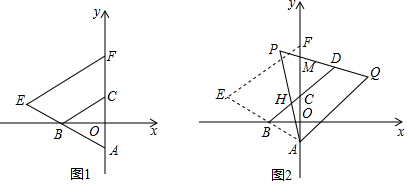
分析 (1)先利用銳角三角函數(shù)即可得出∠BAO=60°,進(jìn)而得出△ABC是等邊三角形,最后用平行線的性質(zhì)即可得出結(jié)論;
(2)先用待定系數(shù)法求出直線BC解析式,即可得出點(diǎn)D坐標(biāo),進(jìn)而求出CD=2,根據(jù)∠DCM=60°構(gòu)造出等邊三角形,進(jìn)而判斷出△ACH≌△DMN,最后代換即可得出結(jié)論.
解答 解:(1)∵A(0,-1),
∴OA=2,
在Rt△AOB中,AB=2,OA=1,
∴cos∠BAO=$\frac{OA}{AB}$=$\frac{1}{2}$,
∴∠BAO=60°,
∵A、C關(guān)于x軸對(duì)稱,
∴C(0,1),
∴AC=2=AB,
∴△ABC是等邊三角形,
∴∠ABC=60°,
∵EF∥BC,
∴∠AEF=∠ABC=60°;
(2)AM+DH大小不發(fā)生變化,
理由:如圖,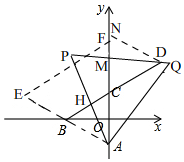 在Rt△AOB中,AB=2,OA=1,根據(jù)勾股定理得,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$,
在Rt△AOB中,AB=2,OA=1,根據(jù)勾股定理得,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$,
∴B(-$\sqrt{3}$,0),
∵C(0,1),
∴直線BC的解析式為y=$\frac{\sqrt{3}}{3}$x+1,
∵D(m,2)在直線BC上,
∴$\frac{\sqrt{3}}{3}$m+1=2,
∴m=$\sqrt{3}$,
∴D($\sqrt{3}$,2),
∴CD=$\sqrt{3+(2-1)^{2}}$=2,
由(1)知,△ABC是等邊三角形,
∴∠ACB=∠ABC=60°,
在AC上取一點(diǎn)N使CN=CD=2,
∴△CDN是等邊三角形,
∴DN=CD=2,∠DNM=∠CDN=60°=∠ACH,
∴∠PDB+∠PDN=60°,
∵△AEF繞A點(diǎn)順時(shí)針旋轉(zhuǎn)得到△APQ,
∴∠P=∠AEF=60°=∠ABC,
∵∠DHP=∠AHB,
∴∠PAB=∠PDB,
∴∠PDN+∠PAB=60°,
∵∠BAC=60°,
∴∠PAC+∠PAB=60°,
∴∠PAC=∠PDN,
∵AC=2=DN,
在△ACH和△DMN中,$\left\{\begin{array}{l}{∠ACH=∠DNM=60°}\\{AC=DN}\\{∠CAH=∠NDM}\end{array}\right.$,
∴△ACH≌△DMN(ASA),
∴CH=MN.
∴AM=AN-MN=CN+AC-MN=2+2-MN=4-MN,
∵DH=CD+CH=2+MN,
∴AM+DH=4-MN+2-MN=6.
即:AM+DH不發(fā)生變化,是定值為6.
點(diǎn)評(píng) 此題是幾何變換綜合題,主要考查了旋轉(zhuǎn)的性質(zhì),銳角三角函數(shù),等邊三角形的判定和性質(zhì),全等三角形的判定和性質(zhì),待定系數(shù)法,勾股定理等知識(shí)點(diǎn);構(gòu)造出等邊△CDN是解本題的關(guān)鍵.


 習(xí)題精選系列答案
習(xí)題精選系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源:2017屆江蘇省無(wú)錫市九年級(jí)下學(xué)期第一次模擬考試數(shù)學(xué)試卷(解析版) 題型:填空題
分解因式:: 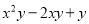 ==______________.
==______________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
| 收費(fèi)方式 | 月使用費(fèi)(元) | 包時(shí)上網(wǎng)時(shí)間(h) | 超時(shí)費(fèi)(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| 0≤x<25 | 25<x≤50 | x>50 | |
| 收費(fèi)方式A應(yīng)收取費(fèi)用(元) | 30 | 3x-45 | 3x-45 |
| 收費(fèi)方式B應(yīng)收取費(fèi)用(元) | 50 | 50 | 3x-100 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
 如圖,正方形ABCD的四個(gè)頂點(diǎn)分別在四條平行線l1,l2,l3,l4上,AD,BC邊分別與l2,l3相交于點(diǎn)F,E,這四條直線中相鄰兩條之間的距離依次為a,b,c(a>0,b>0,c>0),且AB邊于直線l2的夾角為α,則下列結(jié)論錯(cuò)誤的是( )
如圖,正方形ABCD的四個(gè)頂點(diǎn)分別在四條平行線l1,l2,l3,l4上,AD,BC邊分別與l2,l3相交于點(diǎn)F,E,這四條直線中相鄰兩條之間的距離依次為a,b,c(a>0,b>0,c>0),且AB邊于直線l2的夾角為α,則下列結(jié)論錯(cuò)誤的是( )| A. | a=c | B. | 當(dāng)a=b=c時(shí),四邊形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面積為(a+b)2+c2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
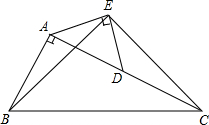 已知:如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點(diǎn)D是AC的中點(diǎn),以AD為斜邊在△ABC外作等腰直角三角形AED,連結(jié)BE、EC.試猜想線段BE和EC有何關(guān)系,并證明你的猜想.
已知:如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點(diǎn)D是AC的中點(diǎn),以AD為斜邊在△ABC外作等腰直角三角形AED,連結(jié)BE、EC.試猜想線段BE和EC有何關(guān)系,并證明你的猜想.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 等腰三角形 | B. | 等邊三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com