
 如圖所示,由1開始連續自然數組成,觀察規律,并完成以下各題.
如圖所示,由1開始連續自然數組成,觀察規律,并完成以下各題.分析 (1)數為自然數,每行數的個數為1,3,5,…的奇數列,最后一數為行數的平方,很容易得到所求之數;
(2)知第n行最后一數為n2,則第一個數為n2-2n+2,每行數由題意知每行數的個數為1,3,5,…的奇數列,故個數為2n-1;
(3)通過以上兩步列公式代入求值,從而解得.
解答 解:(1)由題意知每行最后一數是行數的平方,
所以第8行最后一個數是該行數8的平方即得64,
每行數的個數為1,3,5,…的奇數列,則第8行共有15個數;
(2)由(1)知第n-1行最后一數為(n-1)2,第n行第一個數比它大1,
故第n行第一個數為:(n-1)2+1,即n2-2n+2;
最后一數為:n2
每行數由題意知每行數的個數為1,3,5,…的奇數列,故個數為2n-1;
(3)第n行各數之和:$\frac{{n}^{2}-2n+2+{n}^{2}}{2}×(2n-1)$=(n2-n+1)(2n-1)
當n=10時,(n2-n+1)(2n-1)=(102-10+1)×(2×10-1)=1729.
故答案為:(1)64,8,15;
(2)n2-2n+2,n2,2n-1.
點評 本題考查了數字的規律,(1)看數的規律,自然數的排列,每排個數1,3,5,…從而求得;(2)最后一數是行數的平方,則第一個數即求得;(3)通過以上兩步列公式從而解得,本題看規律為關鍵.


科目:初中數學 來源: 題型:選擇題
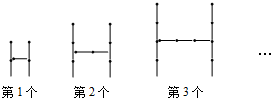 用火柴棍按如圖所示的方式擺大小不同的“H”,依此規律,擺出第n個“H”需要火柴棍的根數是( )
用火柴棍按如圖所示的方式擺大小不同的“H”,依此規律,擺出第n個“H”需要火柴棍的根數是( )| A. | 2n+3 | B. | 3n+2 | C. | 3n+5 | D. | 4n+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{25}{x}$=$\frac{35}{x-20}$ | B. | $\frac{25}{x-20}$=$\frac{35}{x}$ | C. | $\frac{25}{x}$=$\frac{35}{x+20}$ | D. | $\frac{25}{x+20}$=$\frac{35}{x}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com