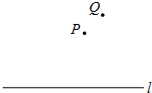Question

12．已知：如圖所示，點P，Q分別代表兩個小區，直線l代表臨近小區的一條公路．點P到直線l的距離為$\frac{3}{2}\sqrt{2}$千米，兩點P、Q所在直線與直線l的夾角為45°，兩小區P、Q之間的距離為1千米．根據居民出行的需要，計劃在公路l上的某處設置一個公交車站．考慮到修路的費用問題，希望車站的位置到小區P和小區Q的距離之和m最短，請在公路l上畫出車站的位置（用點M表示，保留畫圖痕跡，不寫作法），并求出m的值．

Answer 1

分析 如圖，作點P關于直線l的對稱點P′，連接P′Q，交直線l與點M，點M即為所求，由已知條件得到∠QNM=45°，∠PON=90°，PO=$\frac{3}{2}$$\sqrt{2}$，于是得到∠OPN=∠QNM=45°，求得ON=OP=$\frac{3}{2}$$\sqrt{2}$，由對稱的性質得P′N=PN=3，∠MNP′=45°，證得∠QNP′=90°，求出NQ=4，P′Q=5，根據PM=PM，即可得到結論．

解答 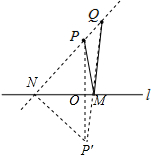解：如圖，作點P關于直線l的對稱點P′，連接P′Q，交直線l與點M，點M即為所求，
如圖，由題意，∠QNM=45°，∠PON=90°，PO=$\frac{3}{2}$$\sqrt{2}$，
∴∠OPN=∠QNM=45°，
∴ON=OP=$\frac{3}{2}$$\sqrt{2}$，
∴PN=3，
由對稱的性質得P′N=PN=3，∠MNP′=45°，
∴∠QNP′=90°，
∵PQ=1，
∴NQ=4，
∴P′Q=5，
∵PM=PM，
∴m=PM+QM=P′M+QM=P′Q=5．

點評 此題主要考查了垂直平分線的作法以及兩點之間線段最短的知識，解答此題的關鍵是熟知軸對稱的性質以及線段垂直平分線上的點到線段兩個端點的距離相等這一性質．