
分析 (1)根據(jù)題意得:k≠0,k-2≠0,k>0,得出k≠0,k≠2,△=4(k-3)2-4k(k-3)>0,求出k=1;
(2)把k=1代入方程得x2-4x-2=0,求出a+b=4,ab=-2,根據(jù)函數(shù)的交點(diǎn)得出ab=n,b=-a+m,即可求出n=-2,m=4,即可得出答案.
解答 解:(1)根據(jù)題意得:k≠0,k-2≠0,k>0,
即k≠0,k≠2,
△=4(k-3)2-4k(k-3)>0,
k<3,
∵k為非負(fù)整數(shù),
∴k只能是1,
即k=1,
(2)把k=1代入方程kx2+2(k-3)x+(k-3)=0得:方程為x2-4x-2=0,
∵a,b是關(guān)于x的一元二次方程kx2+2(k-3)x+(k-3)=0的兩個(gè)根,
∴a+b=4,ab=-2,
∵(a,b)是一次函數(shù)y=(k-2)x+m與反比例函數(shù)y=$\frac{n}{x}$圖象的交點(diǎn),
∴ab=n,b=-a+m,
即a+b=m,
∴n=-2,m=4,
∴一次函數(shù)的解析表達(dá)式是y=-x+4,反比例函數(shù)的解析表達(dá)式是y=-$\frac{2}{x}$.
點(diǎn)評(píng) 本題考查了根與系數(shù)的關(guān)系,根的判別式,用待定系數(shù)法求一次函數(shù)和反比例函數(shù)的解析式的應(yīng)用,主要考查學(xué)生的計(jì)算能力,有一定的難度.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
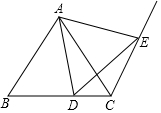 如圖,△ABC是等邊三角形,點(diǎn)D是BC上的點(diǎn),點(diǎn)E是射線CN上的點(diǎn),且CN∥AB,聯(lián)結(jié)AD、AE、DE
如圖,△ABC是等邊三角形,點(diǎn)D是BC上的點(diǎn),點(diǎn)E是射線CN上的點(diǎn),且CN∥AB,聯(lián)結(jié)AD、AE、DE查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
 如圖,四邊形ABCD是⊙O的內(nèi)接四邊形,⊙O的半徑為3,∠B=135°,則$\widehat{AC}$的長(zhǎng)( )
如圖,四邊形ABCD是⊙O的內(nèi)接四邊形,⊙O的半徑為3,∠B=135°,則$\widehat{AC}$的長(zhǎng)( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3}{2}π$ | D. | 2π |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{13}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 東北方向 | B. | 寧波大劇院音樂(lè)廳8排 | ||
| C. | 永豐西路 | D. | 東經(jīng)20度北緯30度 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com