
(本題滿分12分)數學活動——“關于三角形全等的條件”
1.【問題提出】
學習了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我們繼續對“兩個三角形滿足兩邊和其中一邊的對角對應相等”的情形進行研究.
2.【初步思考】
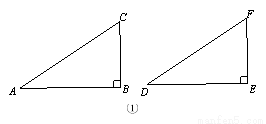
我們不妨將問題用符號語言表示為:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,對∠B進行分類,可分為“∠B是直角、鈍角、銳角”三種情況進行探究.
3.【逐步探究】
(1)第一種情況:當∠B是直角時,如圖①,根據______定理,可得△ABC≌△DEF.
(2)第二種情況:當∠B是鈍角時,△ABC≌△DEF仍成立.請你完成證明.
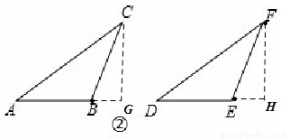
已知:如圖②,△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是鈍角,求證:△ABC≌△DEF.

證明:
(3)第三種情況:當∠B是銳角時,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是銳角,請你用尺規在圖③中作出△DEF,使△DEF和△ABC不全等.(不寫作法,保留作圖痕跡)

4.【深入思考】
∠B還要滿足什么條件,就可以使△ABC≌△DEF?(請直接寫出結論.)
在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是銳角,若∠B _________,則△ABC≌△DEF.
見解析
【解析】
試題分析:(1)對于直角三角形,要判定全等,除了SAS,ASA,AAS,SSS,外還有HL可判定其全等;(2)如圖,過點C作CG⊥AB交AB的延長線于G,過點F作DH⊥DE交DE的延長線于H,要想證明△ABC和△DEF全等,只需證明∠A=∠D,即可,所以證明Rt△ACG和Rt△DFH全等即可,而根據等角的補角相等求出∠CBG=∠FEH,再利用“角角邊”證明△CBG和△FEH全等,根據全等三角形對應邊相等可得CG=FH,從而Rt△ACG和Rt△DFH全等;(3)以點C為圓心,以AC長為半徑畫弧,與AB相交于點D,E與B重合,F與C重合,得到△DEF與△ABC不全等;(4)根據前面的三種情況的結論,可得∠B不小于∠A.
試題解析:3.【逐步探究】
(1)HL 2分
(2)證明:分別作CG⊥AB,FH⊥DE
由∠ABC=∠DEF
得∠CBG=∠FEH4分
又BC=EF,所以可證明△ACG≌△DFH(AAS)
所以CG=FH ,因為AC=DF,
所以Rt△ACG≌Rt△DFH(HL)
所以∠A=∠D,所以△ABC≌△DEF(AAS)
(3)如圖,
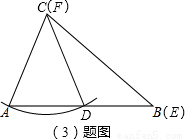
4.【深入思考】∠B≥∠A.
考點:1.全等三角形的判定與性質;2.直角三角形的判定與性質;3.尺規作圖.


科目:初中數學 來源:2014-2015學年江蘇省無錫市八年級上學期期中考試數學試卷(解析版) 題型:解答題
(本題滿分6分)已知a、b為一個等腰三角形的兩條邊長,并滿足:b=2 +
+ +5,求此等腰三角形的周長.
+5,求此等腰三角形的周長.
查看答案和解析>>
科目:初中數學 來源:2016屆山東省七年級上學期期中數學試卷(解析版) 題型:解答題
(本題滿分7分)已知  是關于x的一元一次方程,再解這個方程時,粗心的小成誤把-x看成x,他解得的解是x=4,你知道原方程的正確解釋什么嗎?請寫出解答過程.
是關于x的一元一次方程,再解這個方程時,粗心的小成誤把-x看成x,他解得的解是x=4,你知道原方程的正確解釋什么嗎?請寫出解答過程.
查看答案和解析>>
科目:初中數學 來源:2015屆山東省八年級上學期期中數學試卷(解析版) 題型:選擇題
如下圖,左圖是一個長為2a,寬為2b(a>b)的長方形,用剪刀沿圖中虛線(對稱軸)剪開,把它分成四塊形狀和大小都一樣的小長方形,然后按右圖那樣拼成一個正方形,則中間空的部分的面積是( )
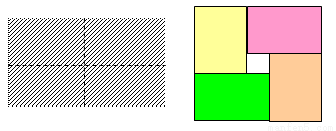
A.2ab B.(a+b)2 C.(a-b)2 D.a2-b2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com