
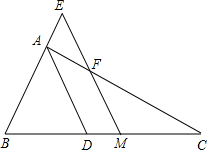
 如圖,△ABC中∠A的平分線為AD,M為BC的中點,過點M作ME∥AD交BA的延長線于E,交AC于F.
如圖,△ABC中∠A的平分線為AD,M為BC的中點,過點M作ME∥AD交BA的延長線于E,交AC于F.分析 (1)過B作BN∥AC交EM延長線于N點,根據(jù)平行線分線段成比例定理可得CF=BN,根據(jù)兩直線平行,內(nèi)錯角相等可得∠CFM=∠N,再根據(jù)平行線的性質(zhì)與角平分線的定義求出∠CFM=∠DAC=∠E,從而得到∠E=∠N,然后證明得到△BEN是等腰三角形即可解決問題
(2)根據(jù)平行線的性質(zhì)求出∠E=∠EFA,根據(jù)等角對等邊的性質(zhì)求出AE=AF,再證明BE=CF=$\frac{1}{2}$(AB+AC),求出CF即可.
解答 (1)證明:過B作BN∥AC交EM延長線于N點,
∵BN∥AC,BM=CM,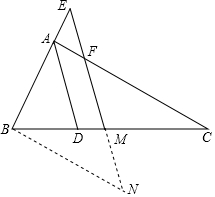
∴CF:BN=CM:BM,∠CFM=∠N,
∴CF=BN,
又∵AD∥ME,AD平分∠BAC,
∴∠CFM=∠DAC=∠E,
∴∠E=∠N,
∴△BEN是等腰三角形,
∴BE=BN=CF,
(2)解:∵∠EFA=∠CFM,
∴∠E=∠EFA,
∴AE=AF,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC,
∵BE=CF,
∴BE=CF=$\frac{1}{2}$(AB+AC)=$\frac{1}{2}$(8+6)=7,
∴AF=AC-FC=8-7=1.
點評 本題考查了等腰三角形的判定與性質(zhì),角平分線的定義,兩直線平行,內(nèi)錯角相等的性質(zhì),兩直線平行,同位角相等的性質(zhì),作輔助線構(gòu)造出等腰三角形是解題的關(guān)鍵,也是本題的難點.


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC 于D,BC=DF.猜想線段AC與EF的數(shù)量關(guān)系,并證明你的結(jié)論.
如圖,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC 于D,BC=DF.猜想線段AC與EF的數(shù)量關(guān)系,并證明你的結(jié)論.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
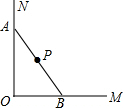 如圖,一根長為a的木棍(AB),斜靠在與地面(OM)垂直的墻上,設木棍的中點為P,若木棍A端沿墻下滑,且B端沿地面向右滑動,在滑動的過程中OP的長度( )
如圖,一根長為a的木棍(AB),斜靠在與地面(OM)垂直的墻上,設木棍的中點為P,若木棍A端沿墻下滑,且B端沿地面向右滑動,在滑動的過程中OP的長度( )| A. | 減小 | B. | 增大 | C. | 不變 | D. | 先減小再增大 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 如圖是二次函數(shù)y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結(jié)論:①b2>4ac;②2a+b=0;③a+b+c=0;④若點B(-$\frac{5}{2}$,y1)、C(-$\frac{1}{2}$,y2)為函數(shù)圖象上的兩點,則y1<y2,其中正確結(jié)論是:①③④(填上序號即可)
如圖是二次函數(shù)y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結(jié)論:①b2>4ac;②2a+b=0;③a+b+c=0;④若點B(-$\frac{5}{2}$,y1)、C(-$\frac{1}{2}$,y2)為函數(shù)圖象上的兩點,則y1<y2,其中正確結(jié)論是:①③④(填上序號即可)查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com