
分析 (1)設(shè)甲公司需x天才能單獨(dú)完成,乙公司需y天才能單獨(dú)完成,根據(jù)工作總量=工作效率×工作時(shí)間結(jié)合“若甲、乙兩個(gè)公司合作,需要6天才能完成;若甲公司單獨(dú)做4天后,剩下的由乙公司來做,還需要9天才能完成”即可得出關(guān)于x、y的二元一次方程組,解之即可得出x、y的值,比較后即可得出結(jié)論;
(2)設(shè)甲公司每天收取安裝費(fèi)a萬元,乙公司每天收取安裝費(fèi)b萬元,根據(jù)總費(fèi)用=單天費(fèi)用×工作時(shí)間結(jié)合“甲、乙兩個(gè)公司合作6天需安裝費(fèi)5.2萬元;甲公司做4天乙公司做9天共需安裝費(fèi)4.8萬元”即可得出關(guān)于a、b的二元一次方程組,解之即可求出a、b的值,再根據(jù)甲、乙單獨(dú)完成需要的天數(shù)求出其總費(fèi)用,比較后即可得出結(jié)論.
解答 解:(1)設(shè)甲公司需x天才能單獨(dú)完成,乙公司需y天才能單獨(dú)完成,
根據(jù)題意得:$\left\{\begin{array}{l}{6(\frac{1}{x}+\frac{1}{y})=1}\\{\frac{4}{x}+\frac{9}{y}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=10}\\{y=15}\end{array}\right.$.
∵10<15,
∴如果從節(jié)約時(shí)間的角度考慮應(yīng)該選擇甲公司.
(2)設(shè)甲公司每天收取安裝費(fèi)a萬元,乙公司每天收取安裝費(fèi)b萬元,
根據(jù)題意得:$\left\{\begin{array}{l}{6(a+b)=5.2}\\{4a+9b=4.8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{5}}\\{b=\frac{4}{15}}\end{array}\right.$.
選甲公司需要的費(fèi)用為10×$\frac{3}{5}$=6(萬元),
選乙公司需要的費(fèi)用為15×$\frac{4}{15}$=4(萬元).
∵6>4,
∴如果從節(jié)約開支的角度考慮應(yīng)該選擇乙公司.
點(diǎn)評 本題考查了二元一次方程組的應(yīng)用,解題的關(guān)鍵是:(1)根據(jù)數(shù)量關(guān)系工作總量=工作效率×工作時(shí)間找出關(guān)于x、y的二元一次方程組;(2)根據(jù)數(shù)量關(guān)系總費(fèi)用=單天費(fèi)用×工作時(shí)間找出關(guān)于a、b的二元一次方程組.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a12=( )3 | B. | a12=( )4 | C. | a12=( )2 | D. | a12=( )6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
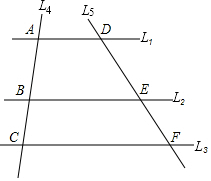 直線L1∥L2∥L3,直線L4被L1,L2,L3所截,其中截得的兩條線段分別為AB,BC.L5是另外一條被L1,L2,L3所截的直線,其中截得的兩條線段分別為DE,EF.小明通過測量得出AB≈1.89cm,BC≈3.80cm,DE≈2.02cm,那么EF約等于4.06cm.
直線L1∥L2∥L3,直線L4被L1,L2,L3所截,其中截得的兩條線段分別為AB,BC.L5是另外一條被L1,L2,L3所截的直線,其中截得的兩條線段分別為DE,EF.小明通過測量得出AB≈1.89cm,BC≈3.80cm,DE≈2.02cm,那么EF約等于4.06cm.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
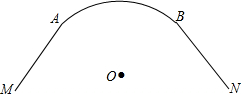 由圓弧形彎道$\widehat{AB}$和兩段直道AM、BN組成的一條公路示意圖如圖所示,直線AM、BN分別與$\widehat{AB}$所在的⊙O相切于點(diǎn)A、B.已知⊙O的半徑為90m,$\widehat{AB}$的長為60πm,求直線AM與BN所成的銳角的度數(shù),以及AM,BN的交點(diǎn)到⊙O的切線長.
由圓弧形彎道$\widehat{AB}$和兩段直道AM、BN組成的一條公路示意圖如圖所示,直線AM、BN分別與$\widehat{AB}$所在的⊙O相切于點(diǎn)A、B.已知⊙O的半徑為90m,$\widehat{AB}$的長為60πm,求直線AM與BN所成的銳角的度數(shù),以及AM,BN的交點(diǎn)到⊙O的切線長.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com