Question

12．已知直線l與⊙O，AB是⊙O的直徑，AD⊥l于點D．
（1）如圖（1），當直線l與⊙O相切于點C時，若∠DAC=35°，求∠DAB的度數；
（2）如圖（2），當直線l與⊙O相交于點E、F時，求證：∠DAE=∠BAF．

Answer 1

分析 （1）連接OC，如圖1，根據切線的性質得OC⊥l，加上AD⊥l，則AD∥OC，所以∠OCA=∠DAC=35°，由于∠OAC=∠OCA=35°，易得∠DAB=70°；
（2）連結BF，如圖2，先根據圓周角定理得到∠AFB=90°，再根據圓內接四邊形的性質得∠AED=∠ABF，然后利用等角的余角相等即可得到結論．

解答 （1）解：連接OC，如圖1，
∵直線l與⊙O相切于點C，
∴OC⊥l，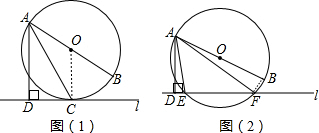
∵AD⊥l，
∴AD∥OC，
∴∠OCA=∠DAC=35°，
∵OA=OC，
∴∠OAC=∠OCA=35°，
∴∠DAB=∠DAC+∠OAC=35°+35°=70°；
（2）證明：連結BF，如圖2，
∵AB是⊙O的直徑，
∴∠AFB=90°，
∵AD⊥EF，
∴∠ADE=90°，
∵∠AED=∠ABF，
∴∠DAE=∠BAF．

點評 本題考查了切線的性質：圓的切線垂直于經過切點的半徑．運用切線的性質來進行計算或論證，常通過作輔助線連接圓心和切點，利用垂直構造直角三角形解決有關問題．