
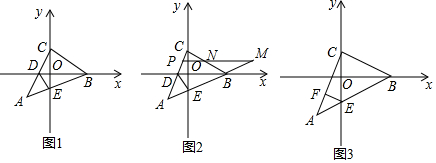
分析 (1)如圖1中,作AF⊥y軸于F,只要證明△ACF≌△CBO,可得AF=OC,CF=OB,由A(-1,-1),推出AF=OF=OC=1,OB=CF=2,由此即可解決問題.
(2)如圖1中,將△AEF繞點A逆時針旋轉90°得到△AMN,只要證明△DAN≌△DAE,可得∠ADN=∠ADE,由∠ADN=∠CDB,推出∠CDB=∠ADE.
(3)由題意直線AC的解析式為y=2x+1,設P(m,2m+1),想辦法求出點M、N的坐標,求出PN、PM即可解決問題.
(4)求出點E坐標,求出AE、AB、BC,根據EF∥BC,得$\frac{EF}{BC}$=$\frac{AE}{AB}$,即可解決問題.
解答 (1)解:如圖1中,作AF⊥y軸于F,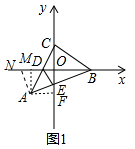
∵∠ACB=∠AFC=∠BOC=90°,
∴∠ACF+∠BCO=90°,∠CAF+∠ACF=90°,
∴∠BCO=∠CAF,
在△ACF和△BCO中,
$\left\{\begin{array}{l}{∠CAF=∠BCO}\\{∠AFC=∠BOC}\\{AC=BC}\end{array}\right.$,
∴△ACF≌△CBO,
∴AF=OC,CF=OB,
∵A(-1,-1),
∴AF=OF=OC=1,OB=CF=2,
∴B(2,0).
(2)如圖1中,將△AEF繞點A逆時針旋轉90°得到△AMN,
∵∠AMO=∠AFO=∠MOF=90°,
∴四邊形AMOF是矩形,
∵AM=AF,
∴四邊形AMOF是正方形,
∵∠CAB=45°,
∴∠EAF+∠MAD=45°=∠NAM+∠MAD=∠NAD,
∴∠NAD=∠EAD,
在△ADN和△ADE中,
$\left\{\begin{array}{l}{AD=AD}\\{∠DAN=∠DAE}\\{AN=AE}\end{array}\right.$,
∵△DAN≌△DAE,
∴∠ADN=∠ADE,
∵∠ADN=∠CDB,
∴∠CDB=∠ADE.
(3)如圖2中,
∵A(-1,-1),C(0,1),
∴直線AC的解析式為y=2x+1,設P(m,2m+1),
∵C(0,1),B(2,0),
∴直線BC的解析式為y=-$\frac{1}{2}$x+1,
∵PM∥x軸,
∴點N與點P的縱坐標相同,2m+1=-$\frac{1}{2}$x+1,
∴x=-4m,
∴N(-4m,2m+1),
∵A(-1,-1),B(2,0),
∴直線AB的解析式為y=$\frac{1}{3}$x-$\frac{2}{3}$,
∵PM∥x軸,
∴點M與點P的縱坐標相同,2m+1=$\frac{1}{3}$x-$\frac{2}{3}$,
∴x=6m+5,
∴M(6m+5,2m+1),
∴PN=-5m,PM=5m+5,
∴PN+PM=-5m+5m+5=5.
(4)如圖3中,
由(3)可知,直線AB的解析式為y=$\frac{1}{3}$x-$\frac{2}{3}$,
∴E(0,-$\frac{2}{3}$),
∵A(-1,-1),B(2,0),C(0,1),
∴AE=$\sqrt{{1}^{2}+(\frac{1}{3})^{2}}$=$\frac{\sqrt{10}}{3}$,AB=$\sqrt{10}$,BC=$\sqrt{5}$,
∵EF∥BC,
∴$\frac{EF}{BC}$=$\frac{AE}{AB}$,
∴$\frac{EF}{\sqrt{5}}$=$\frac{\frac{\sqrt{10}}{3}}{\sqrt{10}}$,
∴EF=$\frac{\sqrt{5}}{3}$.
點評 本題考查三角形綜合題、全等三角形的判定和性質、等腰直角三角形的性質、一次函數的應用、平行線分線段成比例定理等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形,學會利用一次函數求交點坐標,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,在山腳的C處測得山頂A的仰角為53°,沿著坡度為30°的斜坡前進400米到D處(即∠DCB=30°,CD=400米),測得A的仰角為63°,求此山的高度AB.(答案保留根號)
已知:如圖,在山腳的C處測得山頂A的仰角為53°,沿著坡度為30°的斜坡前進400米到D處(即∠DCB=30°,CD=400米),測得A的仰角為63°,求此山的高度AB.(答案保留根號)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com