
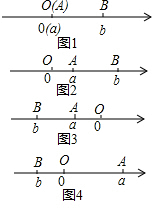
 (1)閱讀下面材料:點A、B在數軸上分別表示實數a、b,A、B兩點之間的距離表示為|AB|.當A、B兩點中有一點在原點時,不妨設點A在原點,如圖1,|AB|=|OB|=|b|=|a-b|,當A、B兩點都不在原點時,
(1)閱讀下面材料:點A、B在數軸上分別表示實數a、b,A、B兩點之間的距離表示為|AB|.當A、B兩點中有一點在原點時,不妨設點A在原點,如圖1,|AB|=|OB|=|b|=|a-b|,當A、B兩點都不在原點時,分析 ①根據兩點間距離公式計算即可.
②根據兩點間距離公式計算,把問題轉化為方程解決.
③當x≤-3時,無解.當-3<x<5時,1<x<5,當x≥5時,不等式恒成立,由此即可解決問題.
④求代數式|x+2|+|x-3|+|x-1|的最小值就是在數軸上找一點P到表示-2,1,3的點的距離之和最小,當P與表示1的點重合時,點P到表示-2,1,3的點的距離之和最小.
解答 解:①數軸上表示1005和-1011的兩點之間的距離是|1005-(-1011)|=2016,
故答案為:2016;
②數軸上分別表示x、-5的兩點A、B之間的距離是|x+5|,
∵|AB|=2,
∴|x+5|=2,
解得:x=-3或-7,
故答案為:|x+5|,-3或-7;
③|x+3|>|x-5|,則相應x的取值范圍是:
當x≤-3時,無解.
當-3<x<5時,1<x<5,
當x≥5時,不等式恒成立,
綜上所述,x的取值范圍為x>1.
故答案為x>1.
④代數式|x+2|+|x-3|+|x-1|的最小值為,
求代數式|x+2|+|x-3|+|x-1|的最小值就是在數軸上找一點P到表示-2,1,3的點的距離之和最小,當P與表示1的點重合時,點P到表示-2,1,3的點的距離之和最小,最小值為5.
故答案為5.
點評 本題考查實數與數軸、絕對值.兩點間距離公式等知識,解題的關鍵是理解題意,把問題轉化為方程解決,學會用絕對值的幾何意義解決實際問題,屬于中考常考題型.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 唐代大詩人李白喜好飲酒作詩,民間有“李白斗酒詩百篇”之說.《算法統宗》中記載了一個“李白沽酒”的故事.詩云:
唐代大詩人李白喜好飲酒作詩,民間有“李白斗酒詩百篇”之說.《算法統宗》中記載了一個“李白沽酒”的故事.詩云:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com