
分析 根據三邊之比設出其中的一條邊長,然后表示出另外兩邊的長,然后利用銳角三角函數的定義求值即可.
解答 解:設BC=x,
∵BC:AC:AB=1:$\sqrt{3}$:2,
∴AC=$\sqrt{3}$x,AB=2x,
∵x2+($\sqrt{3}$x)2=4x2=(2x)2,
∴∠C=90°,
∴cosA+tanA=$\frac{AC}{AB}$+$\frac{BC}{AC}$=$\frac{\sqrt{3}x}{2x}+\frac{x}{\sqrt{3}x}$=$\frac{5\sqrt{3}}{6}$.
點評 本題考查了解直角三角形的知識,解題的關鍵是能夠判定三角形是直角三角形,并正確的運用銳角三角函數的定義列式計算,難度不大.


科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,點D在BC邊上,有下列三個關系式:
如圖,△ABC中,點D在BC邊上,有下列三個關系式:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增減 | +6 | -3 | -8 | +14 | -10 | +15 | -4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
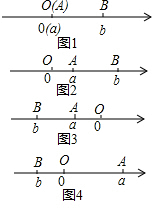 (1)閱讀下面材料:點A、B在數軸上分別表示實數a、b,A、B兩點之間的距離表示為|AB|.當A、B兩點中有一點在原點時,不妨設點A在原點,如圖1,|AB|=|OB|=|b|=|a-b|,當A、B兩點都不在原點時,
(1)閱讀下面材料:點A、B在數軸上分別表示實數a、b,A、B兩點之間的距離表示為|AB|.當A、B兩點中有一點在原點時,不妨設點A在原點,如圖1,|AB|=|OB|=|b|=|a-b|,當A、B兩點都不在原點時,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com