
 一座隧道的截面由拋物線和長方形組成,長方形的長為8m,寬為2m,隧道的最高點P位于AB的中央且距地面6m,建立如圖所示的坐標系.
一座隧道的截面由拋物線和長方形組成,長方形的長為8m,寬為2m,隧道的最高點P位于AB的中央且距地面6m,建立如圖所示的坐標系.分析 (1)由條件可求得拋物線頂點坐標,可設其頂點式,再把C點坐標代入可求得拋物線解析式;
(2)令y=4代入可求得兩點的坐標,再計算兩點間的距離與2的大小關系即可;
(3)利用(2)中所求兩點的距離與4比較大小即可.
解答 解:
(1)由題意可知A(0,2),B(8,2),
∵隧道的最高點P位于AB的中央且距地面6m,
∴P(4,6),
∴可設拋物線解析式為y=a(x-4)2+6,
把A點坐標代入可得2=a(0-4)2+6,解得a=-$\frac{1}{4}$,
∴拋物線解析式為y=-$\frac{1}{4}$(x-4)2+6=-$\frac{1}{4}$x2+2x+2;
(2)由圖象可知當y=2時,x=0或x=8,
∴AB=8>4,
∴一輛貨車高4m,寬2m,能從該隧道內通過;
(3)當雙行道時,則相當于兩輛高4m,寬2m的車,
此時2×4=8,即恰好能通過.
點評 本題主要考查二次函數的性質,掌握二次函數的頂點式是解題的關鍵,即在y=a(x-h)2+k中,對稱軸為x=h,頂點坐標為(h,k).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
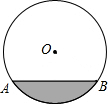 一圓柱形排水管的截面如圖所示,已知排水管的半徑為5m,水面寬AB為8m.由于天氣干燥,水管水面下降,此時排水管水面寬變為6m,求水面下降的高度.
一圓柱形排水管的截面如圖所示,已知排水管的半徑為5m,水面寬AB為8m.由于天氣干燥,水管水面下降,此時排水管水面寬變為6m,求水面下降的高度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在△ABC中,∠ACB=90°,O為邊AB上的一點,以O為圓心,以OA為半徑,作⊙O,交AB于點D,交AC于點E,交BC于點F,且點F恰好是ED的中點,連接DF.
在△ABC中,∠ACB=90°,O為邊AB上的一點,以O為圓心,以OA為半徑,作⊙O,交AB于點D,交AC于點E,交BC于點F,且點F恰好是ED的中點,連接DF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
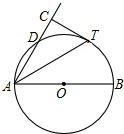 如圖,AB是⊙O直徑,D為⊙O上一點,AT平分∠BAD交⊙O于點T,過T作AD的垂線交AD的延長線于點C.
如圖,AB是⊙O直徑,D為⊙O上一點,AT平分∠BAD交⊙O于點T,過T作AD的垂線交AD的延長線于點C.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com