
 在邊長為3 cm和4 cm的長方形中作等腰三角形,其中等腰三角形的兩個頂點是長方形的頂點,第三個頂點落在長方形的邊上,請作出3種滿足上述條件的等腰三角形(全等的等腰三角形視為一種),并分別求出所畫三角形的面積.
在邊長為3 cm和4 cm的長方形中作等腰三角形,其中等腰三角形的兩個頂點是長方形的頂點,第三個頂點落在長方形的邊上,請作出3種滿足上述條件的等腰三角形(全等的等腰三角形視為一種),并分別求出所畫三角形的面積. 分析 分別作BC、AB的中垂線,由中垂線的性質可得等腰三角形,或以點B為圓心,BA長為半徑畫弧交BC于點F,也可得等腰三角形,最后根據三角形的面積公式可得答案.
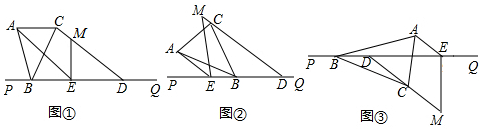
解答 解:如圖1,作BC邊的中垂線,交AD于P,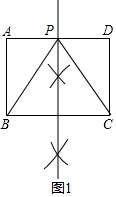
∴PB=PC,即△PBC為等腰三角形,
S△PBC=$\frac{1}{2}$BC×h=$\frac{1}{2}$BC•AB=$\frac{1}{2}$×4×3=6;
如圖2,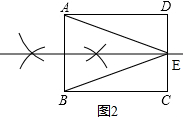
作AB邊的中垂線,交CD于E,
∴EA=EB,即△EAB為等腰三角形,
S△EBC=$\frac{1}{2}$AB×h=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×4×3=6;
如圖3,以點B為圓心,BA長為半徑畫弧交BC于點F,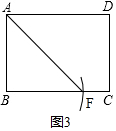
∴BA=BF,即△ABF為等腰三角形,
S△ABF=$\frac{1}{2}$×AB×BF=$\frac{1}{2}$×3×3=4.5.
點評 本題主要考查中垂線的性質及等腰三角形的判定,熟練掌握中垂線的性質是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,點E為BC的中點,若∠B=∠AEF=∠C=90°.連接AF
如圖,點E為BC的中點,若∠B=∠AEF=∠C=90°.連接AF查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 100(1-x)2=64 | B. | 64(1-x)2=100 | C. | 100(1-2x)=64 | D. | 64(1-2x)=100 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
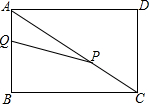 如圖,在矩形ABCD中.AB=3cm.Bc=4cm.動點P以2cm/秒的速度從點C出發,沿CA向點A移動.同時動點Q以1cm/秒的速度從點A出發沿AB向點B移動.設P、Q兩點移動t秒.
如圖,在矩形ABCD中.AB=3cm.Bc=4cm.動點P以2cm/秒的速度從點C出發,沿CA向點A移動.同時動點Q以1cm/秒的速度從點A出發沿AB向點B移動.設P、Q兩點移動t秒.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com