
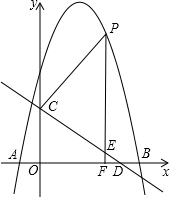
 如圖,拋物線y=ax2+bx+5與x軸交于A(-1,0)、B(5,0)兩點,直線y=-$\frac{3}{4}$x+3與y軸交于點C,與x軸交于點D.點P是拋物線上一動點,過點P作直線PF⊥x軸于點F,交直線CD于點E.設點P的橫坐標為m.
如圖,拋物線y=ax2+bx+5與x軸交于A(-1,0)、B(5,0)兩點,直線y=-$\frac{3}{4}$x+3與y軸交于點C,與x軸交于點D.點P是拋物線上一動點,過點P作直線PF⊥x軸于點F,交直線CD于點E.設點P的橫坐標為m.分析 (1)利用待定系數法求出拋物線的解析式;
(2)用含m的代數式分別表示出PE、EF,然后列方程求解;
(3)解題關鍵是識別出當四邊形PECE′是菱形,然后根據PE=CE的條件,列出方程求解;當四邊形PECE′是菱形不存在時,P點y軸上,即可得到m的值.
解答 解:(1)∵拋物線y=-x2+bx+c與x軸交于A (-1,0),B(5,0)兩點,
∴$\left\{\begin{array}{l}{-1-b+c=0}\\{-25+5b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=4}\\{c=5}\end{array}\right.$,
∴拋物線的解析式為y=-x2+4x+5.
(2)∵點P的橫坐標為m,
∴P(m,-m2+4m+5),E(m,-$\frac{3}{4}$m+3),F(m,0).
∴PE=|yP-yE|=|(-m2+4m+5)-(-$\frac{3}{4}$m+3)|=|-m2+$\frac{19}{4}$m+2|,
EF=|yE-yF|=|(-$\frac{3}{4}$m+3)-0|=|-$\frac{3}{4}$m+3|.
由題意,PE=5EF,即:|-m2+$\frac{19}{4}$m+2|=5|-$\frac{3}{4}$m+3|=|-$\frac{15}{4}$m+15|
①若-m2+$\frac{19}{4}$m+2=-$\frac{15}{4}$m+15,整理得:2m2-17m+26=0,
解得:m=2或m=$\frac{13}{2}$;
②若-m2+$\frac{19}{4}$m+2=-(-$\frac{15}{4}$m+15),整理得:m2-m-17=0,
解得:m=$\frac{1+\sqrt{69}}{2}$或m=$\frac{1-\sqrt{69}}{2}$.
由題意,m的取值范圍為:-1<m<5,故m=$\frac{13}{2}$、m=$\frac{1-\sqrt{69}}{2}$這兩個解均舍去.
∴m=2或m=$\frac{1+\sqrt{69}}{2}$.
∴點F的坐標為(2,0)或($\frac{1+\sqrt{69}}{2}$,0).
(3)假設存在.
作出示意圖如下: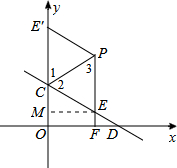
∵點E、E′關于直線PC對稱,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y軸,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四邊形PECE′是菱形.
當四邊形PECE′是菱形存在時,
由直線CD解析式y=-$\frac{3}{4}$x+3,可得OD=4,OC=3,由勾股定理得CD=5.
過點E作EM∥x軸,交y軸于點M,易得△CEM∽△CDO,
∴$\frac{ME}{OD}$=$\frac{CE}{CD}$,即 $\frac{|m|}{2}$=$\frac{CE}{5}$,解得CE=$\frac{5}{4}$|m|,
∴PE=CE=$\frac{5}{4}$|m|,又由(2)可知:PE=|-m2+$\frac{19}{4}$m+2|
∴|-m2+$\frac{19}{4}$m+2|=$\frac{5}{4}$|m|.
①若-m2+$\frac{19}{4}$m+2=$\frac{5}{4}$m,整理得:2m2-7m-4=0,解得m=4或m=-$\frac{1}{2}$;
②若-m2+$\frac{19}{4}$m+2=-$\frac{5}{4}$m,整理得:m2-6m-2=0,解得m1=3+$\sqrt{11}$,m2=3-$\sqrt{11}$.
由題意,m的取值范圍為:-1<m<5,故m=3+$\sqrt{11}$這個解舍去.
當四邊形PECE′是菱形這一條件不存在時,
此時P點橫坐標為0,E,C,E'三點重合與y軸上,也符合題意,
∴P(0,5)
綜上所述,存在滿足條件的m的值為0或-$\frac{1}{2}$或4或3+$\sqrt{11}$.
點評 本題考查二次函數壓綜合題、一次函數的圖象與性質、點的坐標、待定系數法、菱形、相似三角形等知識,解題的關鍵是學會用分類討論思想與方程思想解決問題,解題時注意不能漏解.


科目:初中數學 來源: 題型:選擇題
 如圖所示,在△ABC中,∠ABC=40°,AD,CD分別平分∠BAC,∠ACB,則∠ADC等于( )
如圖所示,在△ABC中,∠ABC=40°,AD,CD分別平分∠BAC,∠ACB,則∠ADC等于( )| A. | 110° | B. | 100° | C. | 190° | D. | 120° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
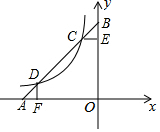 如圖,直線y1=x+b與x軸、y軸分別交于A,B兩點,與反比例函數y2=-$\frac{5}{x}$(x<0)交于C,D兩點,點C的橫坐標為-1,過點C作CE⊥y軸于點E,過點D作DF⊥x軸于點F.下列說法:①b=6;②BC=AD;③五邊形CDFOE的面積為35;④當x<-1時,y1>y2,其中正確的有( )
如圖,直線y1=x+b與x軸、y軸分別交于A,B兩點,與反比例函數y2=-$\frac{5}{x}$(x<0)交于C,D兩點,點C的橫坐標為-1,過點C作CE⊥y軸于點E,過點D作DF⊥x軸于點F.下列說法:①b=6;②BC=AD;③五邊形CDFOE的面積為35;④當x<-1時,y1>y2,其中正確的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com