
問題探究:
(一)新知學習:
圓內接四邊形的判斷定理:如果四邊形對角互補,那么這個四邊形內接于圓(即如果四邊形EFGH的對角互補,那么四邊形EFGH的四個頂點E、F、G、H都在同個圓上).
(二)問題解決:
已知⊙O的半徑為2,AB,CD是⊙O的直徑.P是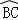 上任意一點,過點P分別作AB,CD的垂線,垂足分別為N,M.
上任意一點,過點P分別作AB,CD的垂線,垂足分別為N,M.
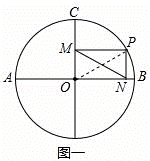
(1)若直徑AB⊥CD,對于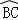 上任意一點P(不與B、C重合)(如圖一),證明四邊形PMON內接于圓,并求此圓直徑的長;
上任意一點P(不與B、C重合)(如圖一),證明四邊形PMON內接于圓,并求此圓直徑的長;
(2)若直徑AB⊥CD,在點P(不與B、C重合)從B運動到C的過程匯總,證明MN的長為定值,并求其定值;
(3)若直徑AB與CD相交成120°角.
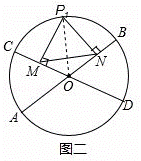
①當點P運動到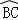 的中點P1時(如圖二),求MN的長;
的中點P1時(如圖二),求MN的長;
②當點P(不與B、C重合)從B運動到C的過程中(如圖三),證明MN的長為定值.
(4)試問當直徑AB與CD相交成多少度角時,MN的長取最大值,并寫出其最大值.

解:(1)如圖一,
∵PM⊥OC,PN⊥OB,
∴∠PMO=∠PNO=90°,
∴∠PMO+∠PNO=180°,
∴四邊形PMON內接于圓,直徑OP=2;
(2)如圖一,
∵AB⊥OC,即∠BOC=90°,
∴∠BOC=∠PMO=∠PNO=90°,
∴四邊形PMON是矩形,
∴MN=OP=2,
∴MN的長為定值,該定值為2;
(3)①如圖二,
∵P1是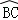 的中點,∠BOC=120°
的中點,∠BOC=120°
∴∠COP1=∠BOP1=60°,∠MP1N=60°.
∵P1M⊥OC,P1N⊥OB,
∴P1M=P1N,
∴△P1MN是等邊三角形,
∴MN=P1M.
∵P1M=OP1•sin∠MOP1=2×sin60°= ,
,
∴MN= ;
;
②設四邊形PMON的外接圓為⊙O′,連接NO′并延長,
交⊙O′于點Q,連接QM,如圖三,
則有∠QMN=90°,∠MQN=∠MPN=60°,
在Rt△QMN中,sin∠MQN= ,
,
∴MN=QN•sin∠MQN,
∴MN=OP•sin∠MQN=2×sin60°=2×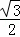 =
= ,
,
∴MN是定值.
(4)由(3)②得MN=OP•sin∠MQN=2sin∠MQN.
當直徑AB與CD相交成90°角時,∠MQN=180°﹣90°=90°,MN取得最大值2.



 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案科目:初中數學 來源: 題型:
全民健身和醫療保健是社會普遍關注的問題,2014年,某社區共投入30萬元用于購買健身器材和藥品.
(1)若2014年社區購買健身器材的費用不超過總投入的 ,問2014年最低投入多少萬元購買藥品?
,問2014年最低投入多少萬元購買藥品?
(2)2015年,該社區購買健身器材的費用比上一年增加50%,購買藥品的費用比上一年減少 ,但社區在這兩方面的總投入仍與2014年相同.
,但社區在這兩方面的總投入仍與2014年相同.
①求2014年社區購買藥品的總費用;
②據統計,2014年該社區積極健身的家庭達到200戶,社區用于這些家庭的藥品費用明顯減少,只占當年購買藥品總費用的 ,與2014年相比,如果2015年社區內健身家庭戶數增加的百分比與平均每戶健身家庭的藥品費用降低的百分比相同,那么,2015年該社區用于健身家庭的藥品費用就是當年購買健身器材費用的
,與2014年相比,如果2015年社區內健身家庭戶數增加的百分比與平均每戶健身家庭的藥品費用降低的百分比相同,那么,2015年該社區用于健身家庭的藥品費用就是當年購買健身器材費用的 ,求2015年該社區健身家庭的戶數.
,求2015年該社區健身家庭的戶數.
查看答案和解析>>
科目:初中數學 來源: 題型:
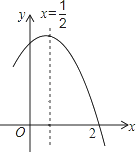
如圖是二次函數y=ax2+bx+c(a≠0)圖象的一部分,對稱軸為x= ,且經過點(2,0),有下列說法:
,且經過點(2,0),有下列說法: ①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是拋物線上的兩點,則y1=y2.上述說法正確的是( )
①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是拋物線上的兩點,則y1=y2.上述說法正確的是( )
|
| A. | ①②④ | B. | ③④ | C. | ①③④ | D. | ①② |
查看答案和解析>>
科目:初中數學 來源: 題型:
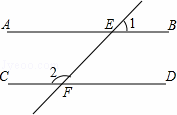
如圖,AB∥CD,直線EF分別交直線AB,CD于點E,F.若∠1=46°30′,則∠1的度數為( )
|
| A. | 43°30′ | B. | 53°30′ | C. | 133°30′ | D. | 153°30′ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com