
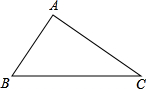
 如圖,已知在△ABC中,∠A=90°.
如圖,已知在△ABC中,∠A=90°.分析 (1)作角B的平分線,與AC的交點就是圓心P,此時⊙P與AB,BC兩邊都相切;
如圖,作BC的垂線PD,證明PD和半徑相等即可,根據(jù)角平分線的性質(zhì)可得:PA=PD.
(2)根據(jù)角平分線得∠PBA=30°,根據(jù)30°角的正切求圓P的半徑AP的長,代入面積公式可以求⊙P的面積.
解答  解:(1)作法:①作∠ABC的平分線BP,交AC于P,
解:(1)作法:①作∠ABC的平分線BP,交AC于P,
②以P為圓心,以PA為半徑作圓,
則⊙P就是符合條件的圓;
證明:過P作PD⊥BC于D,
∵∠BAC=90°,
∴⊙P與AB相切,
∵BP平分∠ABC,
∴AP=PD
∵⊙P的半徑是PA,
∴PD也是⊙P的半徑,即⊙P與BC也相切;
(2)∵∠ABC=60°,BP平分∠ABC,
∴∠ABP=30°,
∴tan30°=$\frac{PA}{AB}$,
∴PA=AB•tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∴⊙P的面積=π×(2$\sqrt{3}$)2=12π,
故答案為:12π.
點評 本題考查了切線的判定和圓的作圖題,切線必須滿足兩個條件:a、經(jīng)過半徑的外端;b、垂直于這條半徑,否則就不是圓的切線.掌握切線的判定方法:①無交點,作垂線段,證半徑;②有交點,作半徑,證垂直;本題利用了第①種判定方法.


科目:初中數(shù)學 來源: 題型:填空題
 如圖,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分線,DE⊥AB于E,若AB=10cm,AC=BC=5$\sqrt{2}$cm,則△DBE的周長等于10cm.
如圖,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分線,DE⊥AB于E,若AB=10cm,AC=BC=5$\sqrt{2}$cm,則△DBE的周長等于10cm.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知在△ABC中,∠A=90°.
如圖,已知在△ABC中,∠A=90°.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | -8-2×6=(-8-2)×6 | B. | 2÷$\frac{4}{3}$×$\frac{3}{4}$=2÷($\frac{4}{3}$×$\frac{3}{4}$) | ||
| C. | (-1)2004+(-1)2005=1+(-1)=0 | D. | -(-3 2)=-9 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數(shù)學 來源:2016-2017學年江蘇省七年級下學期第一次月考數(shù)學試卷(解析版) 題型:解答題
計算:
(1)(﹣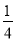 )﹣1+(﹣2)2×50﹣(
)﹣1+(﹣2)2×50﹣(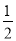 )﹣2;
)﹣2;
(2)(﹣0.5)2014×22015.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com