
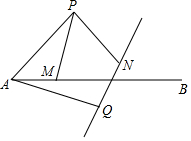
 如圖,點P在射線AB的上方,且∠PAB=45°,PA=2,點M是射線AB上的動點(點M不與點A重合),現將點P繞點A按順時針方向旋轉60°,到點Q,將點M繞點P按逆時針方向旋轉60°到點N,連結AQ,PM,PN,作直線QN.
如圖,點P在射線AB的上方,且∠PAB=45°,PA=2,點M是射線AB上的動點(點M不與點A重合),現將點P繞點A按順時針方向旋轉60°,到點Q,將點M繞點P按逆時針方向旋轉60°到點N,連結AQ,PM,PN,作直線QN.分析 (1)根據旋轉的旋轉判斷出△APQ為等邊三角形,再判斷出∠APM=∠QPN,從而得出△APM≌△QPN即可;
(2)由直線和圓相切得出∠AMP=∠QNP=90°,再用勾股定理即可求出結論;
(3)先判斷出PA=PQ,再判斷出PQ=PN=PM,進而求出∠QPM=30°,即可求出∠QPN=90°,最后用扇形的面積公式即可.
解答 (1)證明:如圖1,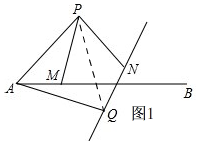 連接PQ,
連接PQ,
由點P繞點A按順時針方向旋轉60°到點Q,
可得,AP=AQ,∠PAQ=60°,
∴△APQ為等邊三角形,
∴PA=PQ,∠APQ=60°,
由點M繞點P按逆時針方向旋轉60°到點N,
可得,PM=PN,∠MPN=60°,
∴∠APM=∠QPN,
則△APM≌△QPN(SAS),
∴AM=QN.
(2)解:存在.
如圖2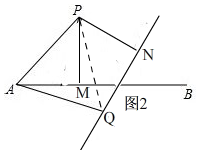 ,由(1)中的證明可知,△APM≌△QPN,
,由(1)中的證明可知,△APM≌△QPN,
∴∠AMP=∠QNP,
∵直線QN與以點P為圓心,以PN的長為半徑的圓相切,
∴∠AMP=∠QNP=90°,
即:PN⊥QN,
在R△APM中,∠PAB=45°,PA=2,
∴AM=$\sqrt{2}$.
(3)解:如圖3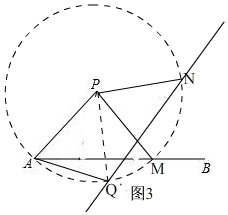 ,由(1)知,△APQ是等邊三角形,
,由(1)知,△APQ是等邊三角形,
∴PA=PQ,∠APQ=60°,
∵以點P為圓心,以PN的長為半徑的圓經過點Q,
∴PN=PQ=PA,
∵PM=PN,
∴PA=PM,
∵∠PAB=45°,
∴∠APM=90°,
∴∠MPQ=∠APM-∠APQ=30°,
∵∠MPN=60°,
∴∠QPN=90°,
∴劣弧NQ與兩條半徑所圍成的扇形的面積是扇形QPN的面積,而此扇形的圓心角∠QPN=90°,半徑為PN=PM=PA=2,
∴劣弧NQ與兩條半徑所圍成的扇形的面積=$\frac{90π•{2}^{2}}{360}$=π.
點評 此題是圓的綜合題,主要考查了旋轉的性質,等邊三角形的判定和性質,全等三角形的判定和性質,切線的性質,扇形的面積公式,解(1)的關鍵是得出PA=PQ,解(2)的關鍵是得出PN⊥QN,解(3)的關鍵是得出PN=PQ=PA,解本題的難點是畫出符合題意的圖形.


 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,長方形ABCD中,AB=3,AD=1,AB在數軸上,若以點A為圓心,AC的長為半徑作弧交數軸于點M,則點M表示的數為( )
如圖,長方形ABCD中,AB=3,AD=1,AB在數軸上,若以點A為圓心,AC的長為半徑作弧交數軸于點M,則點M表示的數為( )| A. | $\sqrt{10}$-1 | B. | $\sqrt{5}$-1 | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2,$\sqrt{3}$,$\sqrt{7}$ | B. | 12,16,20 | C. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | D. | 32,42,52 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
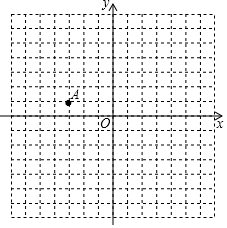 已知一次函數y=-2x-6.
已知一次函數y=-2x-6.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
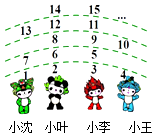 如圖四個小朋友站成一排,老師按圖中所示的規則數數,數到2016時對應的小朋友可得一朵紅花.那么,得紅花的小朋友是( )
如圖四個小朋友站成一排,老師按圖中所示的規則數數,數到2016時對應的小朋友可得一朵紅花.那么,得紅花的小朋友是( )| A. | 小沈 | B. | 小葉 | C. | 小李 | D. | 小王 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
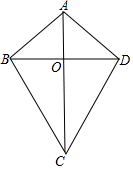 定義:有兩組鄰邊相等的四邊形是箏形
定義:有兩組鄰邊相等的四邊形是箏形查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com