
分析 由點A、B的坐標可得到AB=2$\sqrt{2}$,然后分類討論:若AC=AB;若BC=AB;若CA=CB,確定C點的個數.
解答 解:
∵點A、B的坐標分別為(2,2)、B(4,0).
∴AB=2$\sqrt{2}$,
①若AC=AB,以A為圓心,AB為半徑畫弧與坐標軸有3個交點(含B點),即(0,0)、(4,0)、(0,4),
∵點(0,4)與直線AB共線,
∴滿足△ABC是等腰三角形的C點有1個;
②若BC=AB,以B為圓心,BA為半徑畫弧與坐標軸有2個交點(A點除外),即滿足△ABC是等腰三角形的C點有2個;
③若CA=CB,作AB的垂直平分線與坐標軸有兩個交點,即滿足△ABC是等腰三角形的C點有2個;
綜上所述:點C在坐標軸上,△ABC是等腰三角形,符合條件的點C共有5個.
故答案為:5.
點評 本題主考查了等腰三角形的判定以及分類討論思想的運用,分三種情況分別討論,注意等腰三角形頂角的頂點在底邊的垂直平分線上.


 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:初中數學 來源: 題型:選擇題
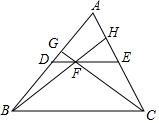 如圖,DE是△ABC的中位線,F為DE上一點,且EF=2DF,BF的延長線交AC于點H,CF的延長線交AB于點G,則S四邊形AGFH:S△BFC=( )
如圖,DE是△ABC的中位線,F為DE上一點,且EF=2DF,BF的延長線交AC于點H,CF的延長線交AB于點G,則S四邊形AGFH:S△BFC=( )| A. | 1:10 | B. | 1:5 | C. | 3:10 | D. | 2:5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com