
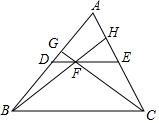
 如圖,DE是△ABC的中位線,F為DE上一點,且EF=2DF,BF的延長線交AC于點H,CF的延長線交AB于點G,則S四邊形AGFH:S△BFC=( )
如圖,DE是△ABC的中位線,F為DE上一點,且EF=2DF,BF的延長線交AC于點H,CF的延長線交AB于點G,則S四邊形AGFH:S△BFC=( )| A. | 1:10 | B. | 1:5 | C. | 3:10 | D. | 2:5 |
分析 設DF=x,EF=2x,S△GDF=S,則DE=3x,由三角形中位線性質得BC=2DE=6x,先證明△GDF∽△GBC,利用相似三角形的性質得S△GBC=36S,則利用三角形面積公式得到S△BGF=6S,S△BFC=30S,接著利用$\frac{HF}{HB}$=$\frac{EF}{BC}$=$\frac{2x}{6x}$=$\frac{HE}{HC}$=$\frac{1}{3}$得到$\frac{HF}{BF}$=$\frac{HE}{EC}$=$\frac{1}{2}$,則S△CFH=$\frac{1}{2}$S△BCF=15S,所以S△BCH=45S,然后利用同樣方法計算出S△BAH=$\frac{1}{3}$S△BCH=15S,于是得到S四邊形AGFH=9S,然后計算S四邊形AGFH:S△BFC的值.
解答 解:設DF=x,EF=2x,S△GDF=S,
則DE=3x,
∵DE是△ABC的中位線,
∴BC=2DE=6x,
∵DE∥BC,
∴△GDF∽△GBC,$\frac{GF}{GC}$=$\frac{DF}{BC}$=$\frac{1}{6}$,
∴$\frac{{S}_{△GDF}}{{S}_{△GBC}}$=($\frac{DF}{BC}$)2,即$\frac{s}{{S}_{GBC}}$=($\frac{x}{6x}$)2=$\frac{1}{36}$,
∴S△GBC=36S,
∵$\frac{{S}_{△BGC}}{{S}_{△GBC}}$=$\frac{GF}{GC}$=$\frac{1}{6}$,
∴S△BGF=6S,
∴S△BFC=30S,
∵EF∥BC,
∴$\frac{HF}{HB}$=$\frac{EF}{BC}$=$\frac{2x}{6x}$=$\frac{HE}{HC}$=$\frac{1}{3}$,
∴$\frac{HF}{BF}$=$\frac{HE}{EC}$=$\frac{1}{2}$,
∴S△CFH=$\frac{1}{2}$S△BCF=15S,
∴S△BCH=45S,
而AE=CE,
∴AH:HC=1:3,
∴S△BAH=$\frac{1}{3}$S△BCH=15S,
∴S四邊形AGFH=S△BAH-S△BGF=15S-6S=9S,
∴S四邊形AGFH:S△BFC=9S:30S=3:10.
故選C.
點評 本題考查了相似三角形的判定與性質:在判定兩個三角形相似時,應注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發揮基本圖形的作用,尋找相似三角形的一般方法是通過作平行線構造相似三角形.在應用相似三角形的性質時,主要利用相似三角形的性質進行幾何計算.也考查了三角形面積公式.


科目:初中數學 來源: 題型:填空題
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 23 | 6 | -3 | -4 | 3 | 18 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
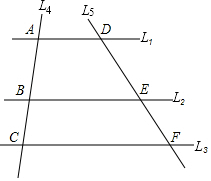 直線L1∥L2∥L3,直線L4被L1,L2,L3所截,其中截得的兩條線段分別為AB,BC.L5是另外一條被L1,L2,L3所截的直線,其中截得的兩條線段分別為DE,EF.小明通過測量得出AB≈1.89cm,BC≈3.80cm,DE≈2.02cm,那么EF約等于4.06cm.
直線L1∥L2∥L3,直線L4被L1,L2,L3所截,其中截得的兩條線段分別為AB,BC.L5是另外一條被L1,L2,L3所截的直線,其中截得的兩條線段分別為DE,EF.小明通過測量得出AB≈1.89cm,BC≈3.80cm,DE≈2.02cm,那么EF約等于4.06cm.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com