
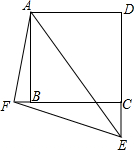
 如圖.在正方形ABCD中,點E,F分別為DC,CB延長線上的點.且滿足∠EAF=45°,∠BAF=15°,連接EF,求證:DE-BF=EF.
如圖.在正方形ABCD中,點E,F分別為DC,CB延長線上的點.且滿足∠EAF=45°,∠BAF=15°,連接EF,求證:DE-BF=EF. 分析 在DE上取一點G,使DG=BF,根據正方形的性質求出∠D=∠ABC=∠ABF=90°,然后利用“邊角邊”證明△ABF和△ADG全等,根據全等三角形對應角相等可得,∠DAG=∠BAF=15°,全等三角形對應邊相等可得AG=AF,然后求出∠BAE的度數以及∠GAE的度數,根據度數求出∠GAE=∠FAE=45°,再利用“邊角邊”證明△AFE和△AGE全等,根據全等三角形對應邊相等可得EF=GE,然后根據圖形邊的關系進行等量代換即可得解.
解答 證明:在DE上取一點G,使DG=BF, 在正方形ABCD中,AD=AB,∠D=∠ABC=∠ABF=90°,
在正方形ABCD中,AD=AB,∠D=∠ABC=∠ABF=90°,
在△ABF和△ADG中,
$\left\{\begin{array}{l}{DG=BF}\\{∠D=∠ABF=90°}\\{AD=AB}\end{array}\right.$,
∴△ABF≌△ADG(SAS),
∴∠DAG=∠BAF=15°,AG=AF,
∵∠EAF=45°,∠BAF=15°,
∴∠BAE=∠EAF-∠BAF=45°-15°=30°,
∴∠GAE=90°-15°-30°=45°,
∴∠GAE=∠FAE=45°,
在△AFE和△AGE中,
$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE=45°}\\{AE=AE}\end{array}\right.$,
∴△AFE≌△AGE(SAS),
∴EF=GE,
∴EF+BF=EG+DG=DE,
∴DE-BF=EF.
點評 本題考查了正方形的性質,全等三角形的判定與性質,題目比較復雜,需要利用二次全等進行證明,作輔助線構造出全等三角形是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,正△ABC的邊長為2,以BC邊上的高AB1為邊作正△AB1C1,△ABC與△AB1C1公共部分的面積記為S1;再以正△AB1C1邊B1C1上的高AB2為邊作正△AB2C2,△AB1C1與△AB2C2公共部分的面積記為S2;…,以此類推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,則Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如圖,正△ABC的邊長為2,以BC邊上的高AB1為邊作正△AB1C1,△ABC與△AB1C1公共部分的面積記為S1;再以正△AB1C1邊B1C1上的高AB2為邊作正△AB2C2,△AB1C1與△AB2C2公共部分的面積記為S2;…,以此類推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,則Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 初三某班學生去中央公園踏青,班級信息員騎自行車先從學校出發,5分鐘后其余同學以60米/分的速度從學校向公園行進,信息員先到達公園后用5分鐘找到聚集地點,再立即按原路以另一速度返回到隊伍匯報聚集地點,最后與同學們一起步行到公園,信息員離其余同學的距離y(米)與信息員出發的時間x(分)之間的關系如圖所示,則信息員開始返回之后,再經過3分鐘與其余同學相距720米.
初三某班學生去中央公園踏青,班級信息員騎自行車先從學校出發,5分鐘后其余同學以60米/分的速度從學校向公園行進,信息員先到達公園后用5分鐘找到聚集地點,再立即按原路以另一速度返回到隊伍匯報聚集地點,最后與同學們一起步行到公園,信息員離其余同學的距離y(米)與信息員出發的時間x(分)之間的關系如圖所示,則信息員開始返回之后,再經過3分鐘與其余同學相距720米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
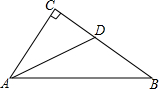 如圖,在△ABC中,∠C=90°,∠CAB的平分線交BC于點D,若AB=5,AC=3,則△DAB的面積為( )
如圖,在△ABC中,∠C=90°,∠CAB的平分線交BC于點D,若AB=5,AC=3,則△DAB的面積為( )| A. | 3 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{25}{8}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com