Question

7．如圖，在矩形ABCD中，E是AD邊的中點(diǎn)，BE⊥AC，垂足為點(diǎn)F，連接DF，有下列五個(gè)結(jié)論：①△AEF∽△CAB；②CF=3AF；③DF=DC；④tan∠CAD=$\sqrt{2}$；③S_△ABF：S_{四邊形BCDF}=1：4．其中．正確的是①③⑤（填序號(hào)）．

Answer 1

分析 ①四邊形ABCD是矩形，BE⊥AC，則∠ABC=∠AFB=90°，又∠BAF=∠CAB，于是△AEF∽△CAB；故①正確；
②由AE=AD=$\frac{1}{2}$BC，又AD∥BC，所以$\frac{AE}{BC}$=$\frac{AF}{FC}$=2；故②錯(cuò)誤；
③過(guò)D作DM∥BE交AC于N，得到四邊形BMDE是平行四邊形，求出BM=DE=$\frac{1}{2}$BC，得到CN=NF，根據(jù)線段的垂直平分線的性質(zhì)可得結(jié)論，故③正確；
④設(shè)AE=a，AB=b，則AD=2a，由△BAE∽△ADC，得出b=$\sqrt{2}$a，進(jìn)而得出tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{2a}$=$\frac{\sqrt{2}}{2}$故④錯(cuò)誤；
⑤由AE∥BC，推出$\frac{AE}{BC}$=$\frac{EF}{BF}$=$\frac{1}{2}$，設(shè)S_△AEF=S_△DEF=m，推出S_△ABF=2m，S_△BFC=4m，S_矩形ABCD=12m，S_矩形BCDF=8m，推出S_△ABF：S_{四邊形BCDF}=1：4，故⑤正確；

解答 解：如圖，過(guò)D作DM∥BE交AC于N，
∵四邊形ABCD是矩形，
∴AD∥BC，∠ABC=90°，AD=BC，
∵BE⊥AC于點(diǎn)F，
∴∠EAC=∠ACB，∠ABC=∠AFE=90°，
∴△AEF∽△CAB，故①正確；

∵AD∥BC，
∴△AEF∽△CBF，
∴$\frac{AE}{BC}$=$\frac{AF}{CF}$，
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC，
∴$\frac{AF}{CF}$=$\frac{1}{2}$，
∴CF=2AF，故②錯(cuò)誤；

∵DE∥BM，BE∥DM，
∴四邊形BMDE是平行四邊形，
∴BM=DE=$\frac{1}{2}$BC，
∴BM=CM，
∴CN=NF，
∵BE⊥AC于點(diǎn)F，DM∥BE，
∴DN⊥CF，
∴DM垂直平分CF，
∴DF=DC，故③正確；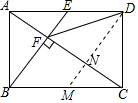

設(shè)AE=a，AB=b，則AD=2a，
由△BAE∽△ADC，有 $\frac{b}{a}$=$\frac{2a}{b}$，即b=$\sqrt{2}$a，
∴tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{2a}$=$\frac{\sqrt{2}}{2}$故④錯(cuò)誤；
∵AE∥BC，
∴$\frac{AE}{BC}$=$\frac{EF}{BF}$=$\frac{1}{2}$，設(shè)S_△AEF=S_△DEF=m，
∴S_△ABF=2m，S_△BFC=4m，S_矩形ABCD=12m，S_矩形BCDF=8m，
∴S_△ABF：S_{四邊形BCDF}=1：4，故⑤正確；
故答案為①③⑤．

點(diǎn)評(píng) 本題主要考查了相似三角形的判定和性質(zhì)，矩形的性質(zhì)，圖形面積的計(jì)算以及解直角三角形的綜合應(yīng)用，正確的作出輔助線構(gòu)造平行四邊形是解題的關(guān)鍵．解題時(shí)注意：相似三角形的對(duì)應(yīng)邊成比例．