
 如圖所示,已知直線l的表達式為y=-$\frac{4}{3}$x+8,且l與x軸、y軸分別交于A、B兩點,動點Q從點B開始在線段BA上以每秒2個單位長度的速度向A移動,同時動點P從點A開始在線段AO上以每秒1個單位長度的速度向點O移動,其中一點停止運動,另一點也隨之停止運動,設點Q、P移動時間為t秒.
如圖所示,已知直線l的表達式為y=-$\frac{4}{3}$x+8,且l與x軸、y軸分別交于A、B兩點,動點Q從點B開始在線段BA上以每秒2個單位長度的速度向A移動,同時動點P從點A開始在線段AO上以每秒1個單位長度的速度向點O移動,其中一點停止運動,另一點也隨之停止運動,設點Q、P移動時間為t秒.分析 (1)根據一次函數圖象上點的坐標特征,即與x軸的交點y=0,與y軸的交點x=0,求出A,B兩點的坐標;
(2)由AO與BO的長,利用勾股定理求出AB的長,根據移動時間為t,表示出AP與AQ,分兩種情況考慮:①由∠QAP=∠BAO,得到△APQ∽△AOB;②由∠QAP=∠BAO,得到△AQP∽△AOB,分別求出t的值即可;
(3)過Q點向x軸引垂線,垂足是M,求得QM,再根據APQ的面積=$\frac{1}{2}$×QM×AP,可以得到△APQ的面積關于t的函數解析式,根據二次函數的性質即可解決問題.
解答 解:(1)∵y=-$\frac{4}{3}$x+8,
令x=0,得y=8;令y=0,得x=6,
∴A,B的坐標分別是(6,0),(0,8);
(2)如圖所示,由BO=8,AO=6,根據勾股定理得AB=$\sqrt{{6}^{2}+{8}^{2}}$=10.
當移動的時間為t時,AP=t,BQ=2t,AQ=10-2t.
∵∠QAP=∠BAO,
∴①當$\frac{PA}{OA}$=$\frac{QA}{BA}$時,△APQ∽△AOB,
此時,$\frac{t}{6}$=$\frac{10-2t}{10}$,
∴t=$\frac{30}{11}$(秒);
∵∠QAP=∠BAO,
②當$\frac{PA}{AB}$=$\frac{AQ}{AO}$時,△APQ∽△AOB,
此時,$\frac{t}{10}$=$\frac{10-2t}{6}$,
∴t=$\frac{50}{13}$(秒),
綜上所述,當t=$\frac{30}{11}$或$\frac{50}{13}$秒時,△APQ與△AOB相似;
(3)如圖所示,過點Q作QM⊥AO于M,則QM∥BO,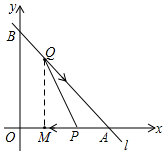
∴△AMQ∽△AOB,
∴$\frac{QM}{BO}$=$\frac{AQ}{AB}$,
即$\frac{QM}{8}$=$\frac{10-2t}{10}$,
解得QM=$\frac{4}{5}$(10-2t),
∴設△APQ的面積為S,則
S=$\frac{1}{2}$×AP×QM
=$\frac{1}{2}$×t×$\frac{4}{5}$(10-2t)
=-$\frac{4}{5}$t2+4t,
∴當t=$\frac{5}{2}$時,S有最大值,且最大值為5,
即當t為$\frac{5}{2}$時,△APQ的面積最大,最大面積是5.
點評 此題屬于相似形綜合題,主要考查了一次函數與坐標軸的交點,二次函數的性質,坐標與圖形性質,相似三角形的判定與性質以及勾股定理的綜合應用,熟練掌握一次函數的性質及相似三角形的對應邊成比例是解本題的關鍵.解題時注意分類思想的靈活運用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
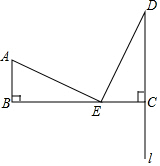 如圖,AB=3,BC=8,AB⊥BC,l⊥BC于點C,點E從B向C運動,過點E作ED⊥AE,交l于D.
如圖,AB=3,BC=8,AB⊥BC,l⊥BC于點C,點E從B向C運動,過點E作ED⊥AE,交l于D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x2+2017=0 | B. | (x+2017)2=0 | C. | (x+1)2=-2017 | D. | (x+2017)(x-2017)=0 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 最大的負有理數是-1 | |
| B. | 任何有理數的絕對值都是正數 | |
| C. | 0是最小的數 | |
| D. | 如果兩個數互為相反數,那么它們的絕對值相等 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
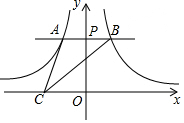 如圖,過y軸上任意一點P,作x軸的平行線,分別與反比例函數$y=-\frac{3}{x}$和$y=\frac{1}{x}$的圖象交于A點和B點,若點C為x軸上任意一點,連接AC、BC,則△ABC的面積為2.
如圖,過y軸上任意一點P,作x軸的平行線,分別與反比例函數$y=-\frac{3}{x}$和$y=\frac{1}{x}$的圖象交于A點和B點,若點C為x軸上任意一點,連接AC、BC,則△ABC的面積為2.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC,垂足為點F,連接DF,有下列五個結論:①△AEF∽△CAB;②CF=3AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;③S△ABF:S四邊形BCDF=1:4.其中.正確的是①③⑤(填序號).
如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC,垂足為點F,連接DF,有下列五個結論:①△AEF∽△CAB;②CF=3AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;③S△ABF:S四邊形BCDF=1:4.其中.正確的是①③⑤(填序號).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com