
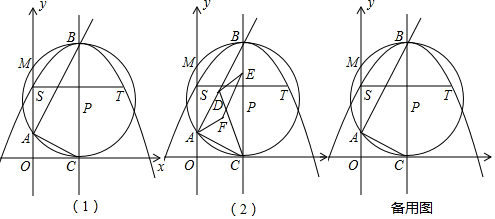
分析 (1)把S(0,6)和點T(8,6)的坐標代入y=-$\frac{1}{4}$x2+bx+c,轉(zhuǎn)化為解方程組即可.
(2)如圖1中,作AH⊥BC于H,則四邊形OAHC是矩形,OA=HC,AH=OC.首先證明點B是拋物線的頂點,B(4,10),C(4,0),設(shè)OA=HC=x,再證明△AHC∽△BHC,可得AH2=CH•BH,即16=x(10-x),解方程即可解決問題.
(3)如圖2中,延長AF交CD于N,連接AE、CD.首先求出直線AB的解析式為y=2x+2,設(shè)D(m,2m+2),由F是△ADC的內(nèi)心,推出點N是CD的中點,推出N(m+2,m+1),推出AF=2FN,推出點F的橫坐標為$\frac{2}{3}$(m+2),因為四邊形ADEN是平行四邊形,所以線段DF的中點的橫坐標與線段AE的中點的橫坐標相同,都是2,可得$\frac{m+\frac{2}{3}(m+2)}{2}$=2,解得m=$\frac{8}{5}$,再想辦法求出點F的坐標即可解決問題.
解答 解:(1)把S(0,6)和點T(8,6)的坐標代入y=-$\frac{1}{4}$x2+bx+c得到$\left\{\begin{array}{l}{c=6}\\{-16+8b+c=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=2}\end{array}\right.$,
∴拋物線的解析式為y=-$\frac{1}{4}$x2+2x+6,.
(2)如圖1中,作AH⊥BC于H,則四邊形OAHC是矩形,OA=HC,AH=OC.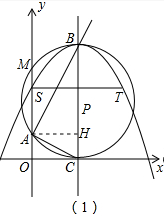
∵S、T關(guān)于對稱軸x=4對稱,BC垂直平分線段ST,
∴點B是拋物線的頂點,B(4,10),C(4,0),設(shè)OA=HC=x
∵BC是直徑,
∴∠BAC=∠AHB=90°,
∴∠CAH+∠BAH=90°,∠BAH+∠ABH=90°,
∴∠CAH=∠ABH,∵∠AHC=∠AHB=90°,
∴△AHC∽△BHC,
∴AH2=CH•BH,
∴16=x(10-x),
解得x=2或8(舍棄),
∴點A坐標(0,2).
(3)如圖2中,延長AF交CD于N,連接AE、CD.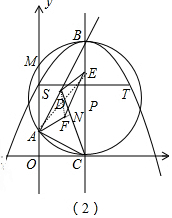
∵A(0,2),B(4,10),
∴直線AB的解析式為y=2x+2,設(shè)D(m,2m+2),
∵F是△ADC的重心,
∴點N是CD的中點,
∴N(m+2,m+1),
∵AF=2FN,
∴點F的橫坐標為$\frac{2}{3}$(m+2),
∵四邊形ADEN是平行四邊形,
∴線段DF的中點的橫坐標與線段AE的中點的橫坐標相同,都是2,
∴$\frac{m+\frac{2}{3}(m+2)}{2}$=2,
解得m=$\frac{8}{5}$,
∴D($\frac{8}{5}$,$\frac{26}{5}$),N($\frac{18}{5}$,$\frac{13}{5}$),
∴直線AN的解析式為y=$\frac{1}{6}$x+2,
∴F($\frac{12}{5}$,$\frac{12}{5}$),
∴AF=$\sqrt{(\frac{12}{5})^{2}+(\frac{12}{5}-2)^{2}}$=$\frac{2\sqrt{37}}{5}$.
點評 本題考查二次函數(shù)綜合題、一次函數(shù)的應用、相似三角形的判定和性質(zhì)、勾股定理、三角形的重心、中點坐標公式等知識,解題的關(guān)鍵是靈活運用所學知識解決問題,學會利用此時想辦法構(gòu)建方程解決問題,屬于中考壓軸題.


科目:初中數(shù)學 來源: 題型:選擇題
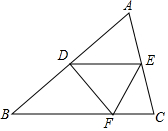 如圖,點D、E分別是邊AB、AC的中點,將△ADE沿著DE對折,點A落在BC邊上的點F,若∠B=50°,則∠BDF的度數(shù)為( )
如圖,點D、E分別是邊AB、AC的中點,將△ADE沿著DE對折,點A落在BC邊上的點F,若∠B=50°,則∠BDF的度數(shù)為( )| A. | 50° | B. | 70° | C. | 75° | D. | 80° |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,已知△ABC與△BDE都是等邊三角形,點D在邊AC上(不與A、C重合),DE與AB相交于點F,則圖中有( )對相似三角形(全等除外)
如圖,已知△ABC與△BDE都是等邊三角形,點D在邊AC上(不與A、C重合),DE與AB相交于點F,則圖中有( )對相似三角形(全等除外)| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,在△ABC中,中線BE,CD相交于點O,連接DE,則下列判斷錯誤的是( )
如圖,在△ABC中,中線BE,CD相交于點O,連接DE,則下列判斷錯誤的是( )| A. | DE是△ABC的中位線 | B. | 點O是△ABC的重心 | ||
| C. | △DEO∽△CBO | D. | $\frac{{S}_{△DOE}}{{S}_{△ADE}}$=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com