
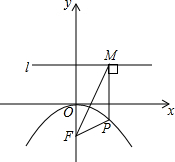
 如圖,拋物線的頂點是原點,拋物線經過A點(8,-8),F點坐標為(0,-2),直線l為y=2,直線l平行于x軸.P點是拋物線上任意一點,過P點作PM⊥l,垂足為M點.
如圖,拋物線的頂點是原點,拋物線經過A點(8,-8),F點坐標為(0,-2),直線l為y=2,直線l平行于x軸.P點是拋物線上任意一點,過P點作PM⊥l,垂足為M點.分析 (1)利用待定系數法即可直接求得二次函數的解析式;
(2)設P的坐標是(x,-$\frac{1}{8}$x2),利用x表示出PM和PF的長,證明PM=PF,根據等邊對等角即可證得;
(3)當△MPF是等腰直角三角形時,根據PM=PF即可列方程求得P的橫坐標.
解答 (1)解:∵二次函數的頂點是原點,
∴設二次函數的解析式是y=ax2,
∴將點A(8,-8)代入得a=-$\frac{1}{8}$,
則二次函數的解析式是y=-$\frac{1}{8}$x2;
(2)證明:∵點P在拋物線y=-$\frac{1}{8}$x2上,
∴設P的坐標是(x,-$\frac{1}{8}$x2),
過點P作PB⊥y軸于點B.
則BF=-2-(-$\frac{1}{8}$x2)=$\frac{1}{8}$x2-2,PB=x.
∴直角△BPF中,PF=$\sqrt{(\frac{1}{8}{x}^{2}-2)^{2}+{x}^{2}}$=$\frac{1}{8}$x2+2.
∵PM⊥直線y=2,
∴PM=$\frac{1}{8}$x2+2,
∴PF=PM,
∴∠PFM=∠PMF;
(3)解:當△MPF是等腰直角三角形時,
PF⊥PM,PF=PM.
設P的橫坐標是x,則2-(-$\frac{1}{8}$x2)=x,
解得:x=4,
則P的坐標是(4,-2).
同理,當P第三象限時,坐標是(-4,-2).
總之,P的坐標是(4,-2)或(-4,-2).
點評 本題考查了待定系數法求二次函數解析式,以及等腰三角形的性質,正確利用P的橫坐標表示出PM和PF的長是關鍵.


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在由邊長為1的小正方形組成的網格圖中有△ABC,建立平面直角坐標系后,點O的坐標是(0,0).
如圖,在由邊長為1的小正方形組成的網格圖中有△ABC,建立平面直角坐標系后,點O的坐標是(0,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com