
 如圖,⊙O的內(nèi)接△ABC中,已知BC=3,∠A=60°,求⊙O的半徑長(zhǎng).
如圖,⊙O的內(nèi)接△ABC中,已知BC=3,∠A=60°,求⊙O的半徑長(zhǎng). 分析 作直徑BD,連接CD,根據(jù)圓周角定理得到∠BCD=90°,設(shè)CD=x,根據(jù)勾股定理列出方程,解方程即可.
解答 解:作直徑BD,連接CD,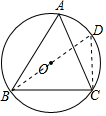
則∠BCD=90°,
∠D=∠A=60°,
∴∠DBC=30°,
設(shè)CD=x,則BD=2x,
由勾股定理得(2x)2=32+x2,
解得x=$\sqrt{3}$,
∴OB=$\frac{1}{2}$BD=x=$\sqrt{3}$,
⊙O的半徑長(zhǎng)$\sqrt{3}$.
點(diǎn)評(píng) 本題考查的是三角形的外接圓和外心的概念和性質(zhì),掌握?qǐng)A周角定理、相似三角形的判定和性質(zhì)是解題的關(guān)鍵.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
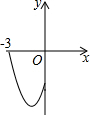 在平面直角坐標(biāo)系中,二次函數(shù)y=x2+2x-3(-3≤x≤0)的圖象如圖所示,點(diǎn)A(x1,y1),B(x2,y2)(x1<x2)是該二次函數(shù)圖象上的兩點(diǎn),則下列結(jié)論中錯(cuò)誤的是②④(填序號(hào))
在平面直角坐標(biāo)系中,二次函數(shù)y=x2+2x-3(-3≤x≤0)的圖象如圖所示,點(diǎn)A(x1,y1),B(x2,y2)(x1<x2)是該二次函數(shù)圖象上的兩點(diǎn),則下列結(jié)論中錯(cuò)誤的是②④(填序號(hào))查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
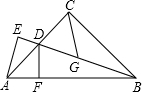 已知:如圖,在△ABC中,∠ACB=90°,AC=BC,BD平分∠ABC,BD交AC于點(diǎn)D,過(guò)點(diǎn)D作DF⊥AB于點(diǎn)F,過(guò)點(diǎn)A作BD的垂線,交BD的延長(zhǎng)線于點(diǎn)E,點(diǎn)G是BD的中點(diǎn).
已知:如圖,在△ABC中,∠ACB=90°,AC=BC,BD平分∠ABC,BD交AC于點(diǎn)D,過(guò)點(diǎn)D作DF⊥AB于點(diǎn)F,過(guò)點(diǎn)A作BD的垂線,交BD的延長(zhǎng)線于點(diǎn)E,點(diǎn)G是BD的中點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
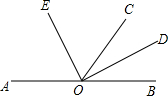 如圖,O是直線AB上的一點(diǎn),OC為任意一條射線,OD平分∠BOC,OE平分∠AOC.
如圖,O是直線AB上的一點(diǎn),OC為任意一條射線,OD平分∠BOC,OE平分∠AOC.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 互余 | B. | 互補(bǔ) | ||
| C. | 既不互余也不互補(bǔ) | D. | 不確定 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
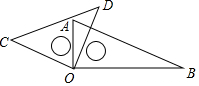 如圖,小明將自己用的一副三角板擺成如圖形狀,下列結(jié)論錯(cuò)誤的是( )
如圖,小明將自己用的一副三角板擺成如圖形狀,下列結(jié)論錯(cuò)誤的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA與∠DOA互余 | D. | ∠AOD與∠COB互補(bǔ) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
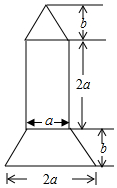 2016年9月15日晚,正值中秋佳節(jié),我國(guó)“天宮二號(hào)”空間實(shí)驗(yàn)室順利升空,這意味著中國(guó)載人航天工程將擁有首個(gè)真正意義的空間實(shí)驗(yàn)室.同學(xué)們倍受鼓舞,如圖是某同學(xué)繪制的火箭模型截面圖,上面是三角形,中間是長(zhǎng)方形,下面是梯形,.
2016年9月15日晚,正值中秋佳節(jié),我國(guó)“天宮二號(hào)”空間實(shí)驗(yàn)室順利升空,這意味著中國(guó)載人航天工程將擁有首個(gè)真正意義的空間實(shí)驗(yàn)室.同學(xué)們倍受鼓舞,如圖是某同學(xué)繪制的火箭模型截面圖,上面是三角形,中間是長(zhǎng)方形,下面是梯形,.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 兩點(diǎn)確定一條直線 | B. | 兩點(diǎn)確定一條線段 | ||
| C. | 兩點(diǎn)之間線段最短 | D. | 兩點(diǎn)之間直線最短 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖所示,小明和小亮用轉(zhuǎn)盤做“配紫色”游戲(紅色和藍(lán)色在一起能配成紫色)小明轉(zhuǎn)動(dòng)的A盤被等分成4個(gè)扇形,小亮轉(zhuǎn)動(dòng)的B盤被等分成3個(gè)扇形,兩人分別轉(zhuǎn)動(dòng)轉(zhuǎn)盤一次.
如圖所示,小明和小亮用轉(zhuǎn)盤做“配紫色”游戲(紅色和藍(lán)色在一起能配成紫色)小明轉(zhuǎn)動(dòng)的A盤被等分成4個(gè)扇形,小亮轉(zhuǎn)動(dòng)的B盤被等分成3個(gè)扇形,兩人分別轉(zhuǎn)動(dòng)轉(zhuǎn)盤一次.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com