Question

12．（1）如圖1，射線OC、OD在∠AOB的內部，射線OM、ON分別平分∠AOD、∠BOC、且∠BON=50°，∠AOM=40°，∠COD=30°，求∠AOB的度數；
（2）如圖2，射線OC、OD在∠AOB的內部，射線OM、ON分別平分∠AOD、∠BOC、且∠AOB=150°，∠COD=30°，求∠MON的度數．

Answer 1

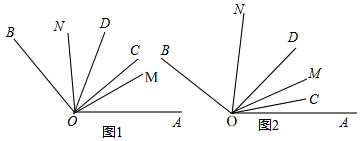
分析 （1）根據角平分線的定義可得出∠AOD、∠BOC的度數，結合∠AOB=∠AOD-∠COD+∠BOC即可得出結論；
（2）根據角平分線的定義可得出∠AOM=$\frac{1}{2}$∠AOD、∠BON=$\frac{1}{2}$∠BOC，由∠AOB=150°、∠COD=30°即可算出∠AOD+∠BOC的度數，再根據∠MON=∠AOB-$\frac{1}{2}$（∠AOD+∠BOC），代入數據即可得出結論．

解答 解：（1）∵射線OM、ON分別平分∠AOD、∠BOC，且∠BON=50°，∠AOM=40°，
∴∠AOD=2∠AOM=80°，∠BOC=2∠BON=100°，
∵∠COD=30°，
∴∠AOB=∠AOD-∠COD+∠BOC=80°-30°+100°=150°．
（2）∵射線OM、ON分別平分∠AOD、∠BOC，
∴∠AOM=$\frac{1}{2}$∠AOD，∠BON=$\frac{1}{2}$∠BOC，
∵∠AOB=150°，∠COD=30°，
∴∠AOD+∠BOC=∠AOB+∠COD=150°+30°=180°，
∴∠MON=∠AOB-（∠BON+∠AOM）=∠AOB-$\frac{1}{2}$（∠AOD+∠BOC）=150°-90°=60°．

點評 本題考查了角的有關計算和角平分線定義的應用，能表示出各個角之間的關系是解此題的關鍵．