
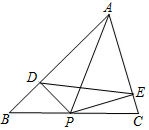
 如圖,在△ABC中,∠B=45°,∠C=75°,BC=6-2$\sqrt{3}$,點P是BC上一動點,PD⊥AB于D,PE⊥AC于E,則線段DE的最小值為$\sqrt{3}$.
如圖,在△ABC中,∠B=45°,∠C=75°,BC=6-2$\sqrt{3}$,點P是BC上一動點,PD⊥AB于D,PE⊥AC于E,則線段DE的最小值為$\sqrt{3}$. 分析 當AP⊥BC時,線段DE的值最小,利用四點共圓的判定可得:A、D、P、E四點共圓,且直徑為AP,得出∠AED=∠B=45°,有一公共角,根據兩角對應相等兩三角形相似得△ADE∽△ACB,則$\frac{AE}{AB}$=$\frac{DE}{CB}$,設AD=2x,表示出AE和AB的長,求出AE與AB的比,代入比例式中,可求出DE的值.
解答 解:當AP⊥BC時,線段DE的值最小,
如圖1,∵PD⊥AB于D,PE⊥AC于E,
∴∠ADP=∠AEP=90°,
∴∠ADP+∠AEP=180°,
∴A、D、P、E四點共圓,且直徑為AP,
在Rt△PBD中,∠B=45°,
∴△PBD是等腰直角三角形,∠APD=45°,
∴△APD也是等腰直角三角形,
∴∠PAD=45°,
∴∠PBD=∠PAD=45°,
∴∠AED=45°,
∴∠AED=∠B=45°,
∵∠EAD=∠CAB,
∴△AED∽△ABC,
∴$\frac{AE}{AB}$=$\frac{DE}{CB}$,
設AD=2x,則PD=DB=2x,AP=2$\sqrt{2}$x,
如圖1,取AP的中點O,連接EO,則AO=OE=OP=$\sqrt{2}$x,
∵∠EAP=∠BAC-∠PAD=60°-45°=15°,
∴∠EOP=2∠EAO=30°,
過E作EM⊥AP于M,則EM=$\frac{\sqrt{2}}{2}$x,
cos30°=$\frac{OM}{OE}$,
∴OM=$\sqrt{2}$x•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{2}$x,
∴AM=$\sqrt{2}$x+$\frac{\sqrt{6}}{2}$x=$\frac{2\sqrt{2}+\sqrt{6}}{2}$x,
由勾股定理得:AE=$\sqrt{A{M}^{2}+E{M}^{2}}$=($\sqrt{3}$+1)x,
∴$\frac{(\sqrt{3}+1)x}{4x}$=$\frac{DE}{6-2\sqrt{3}}$,
∴ED=$\sqrt{3}$.
則線段DE的最小值為$\sqrt{3}$;
故答案為:$\sqrt{3}$.
點評 本題考查了四點共圓,相似三角形的判定和性質,勾股定理,等腰直角三角形的判定和性質,解直角三角形,正確的判斷當AP⊥BC時,線段DE的值最小是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
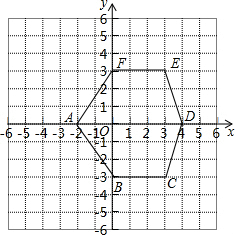 如圖是一個平面直角坐標系,按要求完成下列各小題.
如圖是一個平面直角坐標系,按要求完成下列各小題.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com