
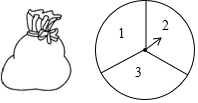
 一個不透明的口袋中裝有4個完全相同的小球,分別標有數字1,2,3,4,另有一個可以自由旋轉的圓盤,被分成面積相等的3個扇形區域,分別標有數字1,2,3(如圖).小穎和小亮想通過游戲來決定誰代表學校參加歌詠比賽,游戲規則為:一人從口袋中摸出一個小球,另一個人轉動圓盤,如果所摸球上的數字與圓盤上轉出數字之和小于4,那么小穎去,否則小亮去.
一個不透明的口袋中裝有4個完全相同的小球,分別標有數字1,2,3,4,另有一個可以自由旋轉的圓盤,被分成面積相等的3個扇形區域,分別標有數字1,2,3(如圖).小穎和小亮想通過游戲來決定誰代表學校參加歌詠比賽,游戲規則為:一人從口袋中摸出一個小球,另一個人轉動圓盤,如果所摸球上的數字與圓盤上轉出數字之和小于4,那么小穎去,否則小亮去.分析 (1)畫樹狀圖展示所有12種等可能性結果,再找出其中數字之和小于4的結果數,然后根據概率公式求解;
(2)利用概率公式計算出P(和不小于4),則P(和小于4)≠P(和不小于4),于是可判斷游戲不公平,改變游戲規則后使數字之和小于4和數字之和不小于4的結果數相等即可.
解答 解:(1)畫樹狀圖: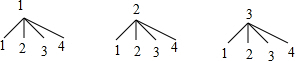
共有12種等可能性結果,其中數字之和小于4的有3種情況,
所以P(和小于4)=$\frac{3}{12}$=$\frac{1}{4}$,
即小穎參加比賽的概率為$\frac{1}{4}$;
(2)該游戲不公平.理由如下:
因為P(和不小于4)=$\frac{3}{4}$,
所以P(和小于4)≠P(和不小于4),
所以游戲不公平,可改為:若數字之和為偶數,則小穎去;若數字之和為奇數,則小亮去.
點評 本題考查了游戲公平性:判斷游戲公平性需要先計算每個事件的概率,然后比較概率的大小,概率相等就公平,否則就不公平.也考查了列表法與樹狀圖法.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
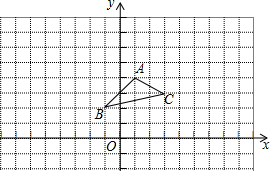 如圖,在平面直角坐標系中,△ABC中的三個頂點坐標分別為A(1,4)、B(-1,2)、C(3,3).在x軸上方,請畫出以原點O為位似中心,相似比為2:1.將△ABC放大后得到的△A1B1C1,并寫出△A1B1C1各頂點的坐標.
如圖,在平面直角坐標系中,△ABC中的三個頂點坐標分別為A(1,4)、B(-1,2)、C(3,3).在x軸上方,請畫出以原點O為位似中心,相似比為2:1.將△ABC放大后得到的△A1B1C1,并寫出△A1B1C1各頂點的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,點A、B、C、D為圓O的四等分點,動點P從圓心O出發,沿線段OC-弧CD-線段DO的路線作勻速運動.設運動時間為t秒,∠APB的度數為y度,則下列圖象中表示y與t的函數關系最恰當的是( )
如圖,點A、B、C、D為圓O的四等分點,動點P從圓心O出發,沿線段OC-弧CD-線段DO的路線作勻速運動.設運動時間為t秒,∠APB的度數為y度,則下列圖象中表示y與t的函數關系最恰當的是( )| A. | 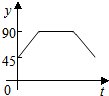 | B. | 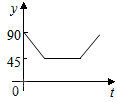 | C. | 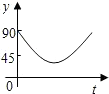 | D. | 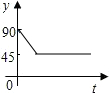 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com