
分析 將原方程整理成一般式得出a、b、c的值,計(jì)算判別式的值,再代入求根公式可得.
解答 解:(1)∵a=1,b=-2,c=-8,
∴△=4-4×1×(-8)=36>0,
則x=$\frac{2±6}{2}$,
∴x=4或x=-2;
(2)∵$\frac{3}{2}$y2+4y-1=0,
∴a=$\frac{3}{2}$,b=4,c=-1,
則△=16-4×$\frac{3}{2}$×(-1)=22>0,
∴x=$\frac{-4±\sqrt{22}}{3}$;
(3)∵3y2-2$\sqrt{3}$y+1=0,
∴a=3,b=-2$\sqrt{3}$,c=1,
則△=12-4×3×1=0,
∴x=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$;
(4)∵a=2,b=-5,c=1,
∴△=25-4×2×1=17>0,
則x=$\frac{5±\sqrt{17}}{4}$;
(5)∵a=-4,b=-8,c=1,
∴△=64-4×(-4)×1=80>0,
則x=$\frac{8±4\sqrt{5}}{-8}$=-$\frac{2±\sqrt{5}}{2}$;
(6)∵a=$\sqrt{2}$,b=-$\sqrt{3}$,c=-$\sqrt{2}$,
∴△=3-4×$\sqrt{2}$×(-$\sqrt{2}$)=11>0,
則x=$\frac{\sqrt{3}±\sqrt{11}}{2\sqrt{2}}$=$\frac{\sqrt{6}±\sqrt{22}}{4}$.
點(diǎn)評(píng) 本題主要考查公式法解一元二次方程,熟練掌握公式法解一元二次方程的步驟和求根公式是解題的關(guān)鍵.


 名牌學(xué)校分層周周測(cè)系列答案
名牌學(xué)校分層周周測(cè)系列答案 黃岡海淀全程培優(yōu)測(cè)試卷系列答案
黃岡海淀全程培優(yōu)測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
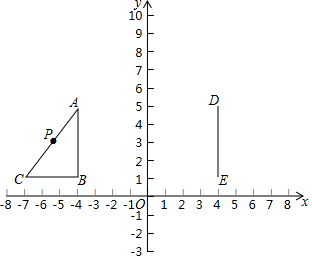 如圖,在平面直角坐標(biāo)系中,Rt△ABC的頂點(diǎn)A(-4,5),B(-4,1),∠B=90°,AC=5,點(diǎn)P是AC的中點(diǎn),線段DE的兩個(gè)端點(diǎn)坐標(biāo)分別為D(4,5),E(4,1).
如圖,在平面直角坐標(biāo)系中,Rt△ABC的頂點(diǎn)A(-4,5),B(-4,1),∠B=90°,AC=5,點(diǎn)P是AC的中點(diǎn),線段DE的兩個(gè)端點(diǎn)坐標(biāo)分別為D(4,5),E(4,1).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
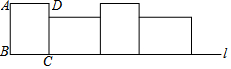 如圖,矩形ABCD中,AB=4,BC=3,將矩形ABCD沿直線l右翻動(dòng)(不滑動(dòng))至如圖位置
如圖,矩形ABCD中,AB=4,BC=3,將矩形ABCD沿直線l右翻動(dòng)(不滑動(dòng))至如圖位置查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
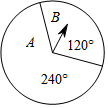 如圖,讓轉(zhuǎn)盤自由轉(zhuǎn)動(dòng)一次,則指針落在A區(qū)域的概率是( )
如圖,讓轉(zhuǎn)盤自由轉(zhuǎn)動(dòng)一次,則指針落在A區(qū)域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 2500(1+x)+2500(1+x)2=3600 | B. | 2500(1+x%)2=3600 | ||
| C. | 2500x2=3600 | D. | 2500(1+x)2=3600 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com