
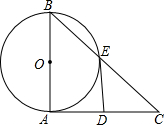
 已知,在Rt△ABC中,∠BAC=90°,以AB為直徑的⊙O與BC相交于點E,在AC上取一點D,使得DE=AD,
已知,在Rt△ABC中,∠BAC=90°,以AB為直徑的⊙O與BC相交于點E,在AC上取一點D,使得DE=AD,分析 (1)連接OE、DE,證明△AOD≌△EOD,得到∠OED=∠BAC=90°,證明結論;
(2)根據全等三角形的性質得到∠AOD=∠EOD,根據三角形的外角的性質得到∠BEO=∠EOD,得到OD∥BC,求出OD,根據勾股定理計算即可.
解答  (1)證明:連接OE、DE,
(1)證明:連接OE、DE,
在△AOD和△EOD中,
$\left\{\begin{array}{l}{OA=OE}\\{DA=DE}\\{OD=OD}\end{array}\right.$,
∴△AOD≌△EOD(SSS),
∴∠OED=∠BAC=90°,
∴DE是⊙O的切線;
(2)解:∵△AOD≌△EOD,
∴∠AOD=∠EOD,
∵OB=OE,
∴∠B=∠OEB,
∵∠AOE=∠B+∠OEB,
∴∠BEO=∠EOD,
∴OD∥BC,又AO=BO,
∴OD=$\frac{1}{2}$BC=5,
由勾股定理得,AO=$\sqrt{O{D}^{2}-A{D}^{2}}$=3,
則⊙O的半徑為3.
點評 本題考查的是切線的判定、全等三角形的判定和性質、三角形中位線定理的應用,掌握經過半徑的外端且垂直于這條半徑的直線是圓的切線是解題的關鍵.


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中.O為坐標原點,直線y=-$\frac{3}{4}$x+3與x軸、y軸分別交于A,B兩點.點P從點A出發,以每秒1個單位的速度沿射線AO勻速運動,設點P的運動時間為t秒.過點P與直線AB垂直的直線與y軸交于點E.
如圖,在平面直角坐標系中.O為坐標原點,直線y=-$\frac{3}{4}$x+3與x軸、y軸分別交于A,B兩點.點P從點A出發,以每秒1個單位的速度沿射線AO勻速運動,設點P的運動時間為t秒.過點P與直線AB垂直的直線與y軸交于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是一塊長、寬、高分別為4cm、2cm和1cm的長方體木塊,一只螞蟻要從長方體木塊的-個頂點A處,沿著長方體木塊的表面爬到長方體木塊上和頂點A相對的頂點B處吃食物,那么它需要爬行的最短路徑的長是5cm.
如圖是一塊長、寬、高分別為4cm、2cm和1cm的長方體木塊,一只螞蟻要從長方體木塊的-個頂點A處,沿著長方體木塊的表面爬到長方體木塊上和頂點A相對的頂點B處吃食物,那么它需要爬行的最短路徑的長是5cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,O為坐標原點,⊙O的半徑為1,點P是直線y=-2x-6上的動點,過點P作⊙O的切線PA、PB,A、B為切點,連接OA、OB,則四邊形OAPB的面積的最小值為$\frac{\sqrt{155}}{5}$.
如圖,O為坐標原點,⊙O的半徑為1,點P是直線y=-2x-6上的動點,過點P作⊙O的切線PA、PB,A、B為切點,連接OA、OB,則四邊形OAPB的面積的最小值為$\frac{\sqrt{155}}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com