
 如圖是一塊長、寬、高分別為4cm、2cm和1cm的長方體木塊,一只螞蟻要從長方體木塊的-個頂點A處,沿著長方體木塊的表面爬到長方體木塊上和頂點A相對的頂點B處吃食物,那么它需要爬行的最短路徑的長是5cm.
如圖是一塊長、寬、高分別為4cm、2cm和1cm的長方體木塊,一只螞蟻要從長方體木塊的-個頂點A處,沿著長方體木塊的表面爬到長方體木塊上和頂點A相對的頂點B處吃食物,那么它需要爬行的最短路徑的長是5cm. 分析 把此長方體的一面展開,然后在平面內,利用勾股定理求點A和B點間的線段長,即可得到螞蟻爬行的最短距離.在直角三角形中,一條直角邊長等于長方體的高,另一條直角邊長等于長方體的長寬之和,利用勾股定理可求得.
解答 解:因為平面展開圖不唯一,故分情況分別計算,進行大、小比較,再從各個路線中確定最短的路線.
(1)展開前面右面由勾股定理得AB2=(2+4)2+12=37;
(2)展開前面上面由勾股定理得AB2=(1+4)2+22=29;
(3)展開左面上面由勾股定理得AB2=(2+1)2+42=25.
所以最短路徑的長為AB=$\sqrt{25}$=5cm.
故答案為:5cm.
點評 本題考查了勾股定理的拓展應用.“化曲面為平面”是解決“怎樣爬行最近”這類問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,經過點B(1,0)的直線y=kx+b與直線y=4x+4相交于點A(m,$\frac{8}{3}$),則0<kx+b<4x+4的解集為( )
如圖,經過點B(1,0)的直線y=kx+b與直線y=4x+4相交于點A(m,$\frac{8}{3}$),則0<kx+b<4x+4的解集為( )| A. | x<$\frac{1}{3}$ | B. | -$\frac{1}{3}$<x<1 | C. | x<1 | D. | -1<x<1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
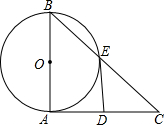 已知,在Rt△ABC中,∠BAC=90°,以AB為直徑的⊙O與BC相交于點E,在AC上取一點D,使得DE=AD,
已知,在Rt△ABC中,∠BAC=90°,以AB為直徑的⊙O與BC相交于點E,在AC上取一點D,使得DE=AD,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com