Question

18．已知三角形兩邊之和是10，這兩邊夾角為30°，面積為$\frac{25}{4}$，求證：此三角形為等腰三角形．

Answer 1

分析 過點A作AD⊥BC于點D，設AC=x（0＜x＜10），則BC=10-x，根據直角三角形中30°角的對邊等于斜邊的一半即可得出AD的值，根據三角形的面積結合△ABC的面積為$\frac{25}{4}$，即可求出x的值，進而可得出10-x的值，由x=10-x=5即可得出AC=BC，由此即可證得此三角形為等腰三角形．

解答 證明：過點A作AD⊥BC于點D，如圖所示．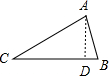
設AC=x（0＜x＜10），則BC=10-x，
∵∠C=30°，AD⊥BC，
∴AD=$\frac{1}{2}$AC=$\frac{1}{2}$x．
∵△ABC的面積為$\frac{25}{4}$，
∴$\frac{1}{2}$BC•AD=$\frac{1}{4}$x²=$\frac{25}{4}$，
解得：x₁=5，x₂=-5（舍去）．
∵x=5，10-x=5，
∴AC=BC，
∴此三角形為等腰三角形．

點評 本題考查了等腰三角形的判定以及三角形的面積，利用三角形的面積公式找出關于x的一元二次方程是解題的關鍵．