
 已知,如圖,拋物線y=-x2+bx+c經過直線y=-x+3與坐標軸的兩個交點A,B,此拋物線與x軸的另一個交點為C,拋物線的頂點為D.
已知,如圖,拋物線y=-x2+bx+c經過直線y=-x+3與坐標軸的兩個交點A,B,此拋物線與x軸的另一個交點為C,拋物線的頂點為D.分析 (1)先求得點A和點B的坐標,然后將點A和點B的坐標代入拋物線的解析式求得b,c的值即可;
(2)設M的坐標為(x,y),由△ACM與△ABC的面積相等可得到|y|=3,將y=3或y=-3代入拋物線的解析式求得對應的x的值,從而得到點M的坐標;
(3)先利用配方法求得點D的坐標,當∠DNA=90°時,DN⊥OA,可得到點N的坐標,從而得到AN=2,然后再求得AD的長;當∠N′DA=90°時,依據sin∠DN′A=sin∠ADN可求得AN′的長,從而可得到N′的解析式.
解答 解:(1)將x=0代入AB的解析式得:y=3,
∴B(0,3).
將y=0代入AB的解析式得:-x+3=0,解得x=3,
A(3,0).
將點A和點B的坐標代入得:$\left\{\begin{array}{l}{c=3}\\{-9+3b+3=0}\end{array}\right.$,
解得:b=2,c=3.
∴拋物線的解析式為y=-x2+2x+3.
(2)設M的坐標為(x,y).
∵△ACM與△ABC的面積相等,
∴$\frac{1}{2}$AC•|y|=$\frac{1}{2}$AB•OB.
∴|y|=OB=3.
當y=3時,-x2+2x+3=3,解得x=0(舍去)或x=2,
∴M(2,3).
當y=-3時,-x2+2x+3=3,解得:x=1+$\sqrt{7}$或x=1-$\sqrt{7}$.
∴M(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3).
綜上所述點M的坐標為(2,3)或(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3).
(3)y=-x2+2x+3=-(x-1)2+4,
∴D(1,4).
①當∠DNA=90°時,如圖所示: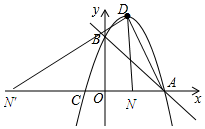
∵∠DNA=90°時,
∴DN⊥OA.
又∵D(1,4)
∴B(1,0).
∴AN=2.
∵DN=4,AN=2,
∴AD=2$\sqrt{5}$.
②當∠N′DA=90°時,則DN′A=∠NDA.
∴$\frac{AD}{AN′}$=$\frac{AN}{AD}$,即$\frac{2\sqrt{5}}{AN′}$=$\frac{2}{2\sqrt{5}}$,解得:AN′=10.
∵A(3,0),
∴N′(-7,0).
綜上所述點N的坐標為(1,0)或(-7,0).
點評 本題主要考查的是二次函數的應用,求得點A和點B的坐標是解答問題(1)的關鍵,求得點M的縱坐標是解答問題(2)的關鍵,求得AN′的長是解答問題(3)的關鍵.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:解答題
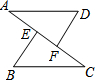 如圖,在△AFD和△CEB中,點A、E、F、C在同一條直線上,有下列四個判斷:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.請以其中三個為已知條件,剩下一個作為結論,編一道數學題(用序號???⇒?的形式寫出),并寫出證明過程.
如圖,在△AFD和△CEB中,點A、E、F、C在同一條直線上,有下列四個判斷:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.請以其中三個為已知條件,剩下一個作為結論,編一道數學題(用序號???⇒?的形式寫出),并寫出證明過程.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
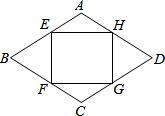 如圖,在菱形ABCD的邊上依次取點E,F,G,H,使AE=AH=CF=CG,若菱長邊長是1,∠A=120°,
如圖,在菱形ABCD的邊上依次取點E,F,G,H,使AE=AH=CF=CG,若菱長邊長是1,∠A=120°,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 6,3$\sqrt{2}$ | B. | 6,3 | C. | 3$\sqrt{2}$,3 | D. | 6$\sqrt{2}$,3$\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com