
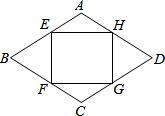
 如圖,在菱形ABCD的邊上依次取點E,F,G,H,使AE=AH=CF=CG,若菱長邊長是1,∠A=120°,
如圖,在菱形ABCD的邊上依次取點E,F,G,H,使AE=AH=CF=CG,若菱長邊長是1,∠A=120°,分析 (1)首先利用菱形的性質得到∠A=∠C,∠B=∠D,AB=BC=CD=DA,然后根據AE=AH=CF=CG,得到BE=BF=DH=DG,從而證得△AEH≌△CGF,△BEF≌△DGH,證得四邊形EFGH是平行四邊形,然后利用有一個角是直角的平行四邊形是矩形判定四邊形EFGH是矩形;
(2)先求出AC=1,再求出BE=1-x,再用三角函數得出PE=$\frac{\sqrt{3}}{2}$x進而得出EH=$\sqrt{3}$x,最后用矩形的面積公式即可得出結論;
(3)由(2)EH=$\sqrt{3}$x,EF=1-x,再用正方形的性質即可建立方程求出x值即可.
解答 (1)證明:∵四邊形ABCD是菱形,
∴∠A=∠C,∠B=∠D,AB=BC=CD=DA
∵AE=AH=CF=CG,
∴BE=BF=DH=DG,
∴△AEH≌△CGF,△BEF≌△DGH,
∴EH=FG,EF=GH,
∴四邊形EFGH是平行四邊形,
∵∠A+∠D=180°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四邊形EFGH是矩形;
(2)解:如圖,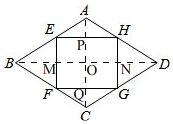 連接AC,交EH,FG于P,Q,連接BD交EF,HG于M,N,
連接AC,交EH,FG于P,Q,連接BD交EF,HG于M,N,
∵四邊形ABCD是菱形,∠BAC=120°,
∴∠ABC=60°,
∴AC=AB=1,
由(1)知,四邊形EFGH是矩形,
∴EF∥AC,
∴EF=BE=AB-AE=1-x,
在Rt△APE中,∠PAE=$\frac{1}{2}$∠BAD=60°,
∴sin∠PAE=$\frac{PE}{AE}$,
∴PE=AEsin∠PAE=x•sin60°=$\frac{\sqrt{3}}{2}$x,
∴EH=2PE=$\sqrt{3}$x,
∴四邊形EFGH的面積是y=EF•EH=(1-x)•$\sqrt{3}$x=-$\sqrt{3}$x2+$\sqrt{3}$x,(0<x<1);
(3)解:由(2)知,EH=$\sqrt{3}$x,EF=1-x,
∵矩形EFGH是正方形,
∴EF=EH,
∴$\sqrt{3}$x=1-x,
∴x=$\frac{\sqrt{3}-1}{2}$.
點評 此題是四邊形綜合題,主要考查了全等三角形的判定和性質,菱形的性質,等邊三角形的判定和性質,矩形的判定,正方形的性質,解(1)的關鍵先判斷四邊形EFGH是平行四邊形,解(2)的關鍵是用x表示EF和
EH,解(3)的關鍵是掌握正方形的性質,是一道中等難度的題目.


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片ABCD,使AD落在BD上,點A恰好與BD上的點F重合,展開后折痕DE分別交AB、AC于點E、G,連結GF,給出下列結論:
如圖,正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片ABCD,使AD落在BD上,點A恰好與BD上的點F重合,展開后折痕DE分別交AB、AC于點E、G,連結GF,給出下列結論:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知,如圖,拋物線y=-x2+bx+c經過直線y=-x+3與坐標軸的兩個交點A,B,此拋物線與x軸的另一個交點為C,拋物線的頂點為D.
已知,如圖,拋物線y=-x2+bx+c經過直線y=-x+3與坐標軸的兩個交點A,B,此拋物線與x軸的另一個交點為C,拋物線的頂點為D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{x+y}{{x}^{2}+xy}$=$\frac{1}{x}$ | C. | $\frac{x+y}{x+y}$=0 | D. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com