
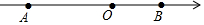 如圖,數軸上有A、B兩點,AB=12,原點O是線段AB上的一點,OA=2OB.
如圖,數軸上有A、B兩點,AB=12,原點O是線段AB上的一點,OA=2OB.分析 (1)由AO=2OB可知,將12平均分成三份,AO占兩份為8,OB占一份為4,由圖可知,A在原點的左邊,B在原點的右邊,從而得出結論;
(2)分兩種情況:①點C在原點的左邊,即在線段OA上時,②點C在原點的右邊,即在線段OB上時,分別根據AC=CO+CB列式即可;
(3)①分兩種情況:點P在原點的左側和右側時,OP表示的代數式不同,OQ=4+t,分別代入2OP-OQ=4列式即可求出t的值;
②點M運動的時間就是點P從點O開始到追到點Q的時間,設點M運動的時間為t秒,列式為t(2-1)=8,解出即可解決問題.
解答 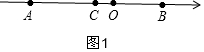 解:(1)∵AB=12,AO=2OB,
解:(1)∵AB=12,AO=2OB,
∴AO=8,OB=4,
∴A點所表示的實數為-8,B點所表示的實數為4;
(2)設C點所表示的實數為x,
分兩種情況:①點C在線段OA上時,則x<0,如圖1,
∵AC=CO+CB,
∴8+x=-x+4-x,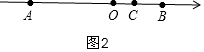
3x=-4,
x=-$\frac{4}{3}$;
②點C在線段OB上時,則x>0,如圖2,
∵AC=CO+CB,
∴8+x=4,
x=-4(不符合題意,舍);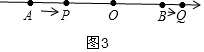
綜上所述,C點所表示的實數是-$\frac{4}{3}$;
(3)①當0<t<4時,如圖3,
AP=2t,OP=8-2t,BQ=t,OQ=4+t,
∵2OP-OQ=4,
∴2(8-2t)-(4+t)=4,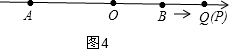
t=$\frac{8}{5}$=1.6,
當點P與點Q重合時,如圖4,
2t=12+t,t=12,
當4<t<12時,如圖5,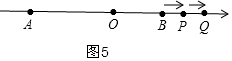
OP=2t-8,OQ=4+t,
則2(2t-8)-(4+t)=4,
t=8,
綜上所述,當t為1.6秒或8秒時,2OP-OQ=4;
②當點P到達點O時,8÷2=4,此時,OQ=4+t=8,即點Q所表示的實數為8,
如圖6,設點M運動的時間為t秒,
由題意得:2t-t=8,
t=8,
此時,點P表示的實數為8×2=16,所以點M表示的實數也是16,
∴點M行駛的總路程為:3×8=24,
答:點M行駛的總路程為24和點M最后位置在數軸上對應的實數為16.
點評 本題考查了數軸上兩點的距離、數軸上點的表示、一元一次方程的應用,比較復雜,要認真理清題意,并注意數軸上的點,原點左邊表示負數,右邊表示正數,在數軸上,兩點的距離等于任意兩點表示的數的差的絕對值.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3a2bc與bca2不是同類項 | B. | $\frac{{m}^{2}n}{5}$和$\frac{a+b}{2}$都是單項式 | ||
| C. | 單項式-x3y2的次數是3,系數是-1 | D. | 3x2-y+2xy2是三次三項式 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
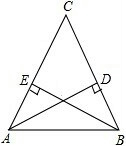 如圖,從C地看A,B兩地的視角∠C是銳角,從C地到A,B兩地的距離相等,A地到路段BC的距離AD與B地到路段AC的距離BE相等嗎?為什么?
如圖,從C地看A,B兩地的視角∠C是銳角,從C地到A,B兩地的距離相等,A地到路段BC的距離AD與B地到路段AC的距離BE相等嗎?為什么?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
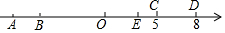 如圖,數軸上有A、B、C、D、O五個點,點O為原點,點C在數軸上表示的數是5,線段CD的長度為3個單位,線段AB的長度為1個單位,且B、C兩點之間的距離為12個單位,請解答下列問題:
如圖,數軸上有A、B、C、D、O五個點,點O為原點,點C在數軸上表示的數是5,線段CD的長度為3個單位,線段AB的長度為1個單位,且B、C兩點之間的距離為12個單位,請解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
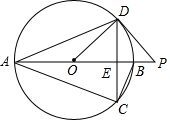 已知:如圖,AB是⊙O的直徑,CD是弦,且AB⊥CD于E,P是AB延長線上一點,連接PD,∠PDC=∠CAD.
已知:如圖,AB是⊙O的直徑,CD是弦,且AB⊥CD于E,P是AB延長線上一點,連接PD,∠PDC=∠CAD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | ∠A=∠E | D. | ∠B=∠D |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com