
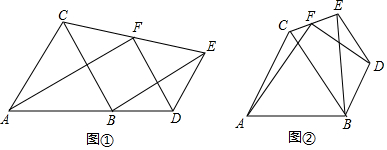
 如圖①,△ABC為等邊三角形,D為AB延長線上一點,BD=DE.∠BDE=120°,連接EB、EC,F為EC的中點,連接FA、FD.
如圖①,△ABC為等邊三角形,D為AB延長線上一點,BD=DE.∠BDE=120°,連接EB、EC,F為EC的中點,連接FA、FD.分析 (1)方法一:利用倍長中線法得出△CFM≌△EFD,進而得出FM=FD,再判斷出AM=AD,最后利用等腰三角形的三線合一即可即可得出結論;
方法二:先判斷出∠CBE=90°,再利用直角三角形斜邊的中線等于斜邊的一半,得出BF=EF=CF,進而判斷出△BDF≌△EDF,△ABF≌△ACF,最后代換即可得出結論.
(2)利用倍長中線法得出△CFM≌△EFD,即CM=DE,由旋轉的性質進而判斷出點M,C,B在同一條直線上,進而判斷出△ACM≌△ABD,即可同(1)的方法得出結論;
(3)同(2)的方法得出CM=BD,∠MCF=∠DEF再用周角的定義,三角形的內角和得出∠ACM=∠ABD,即可判斷出△ACM≌△ABD,最后同(2)的方法得出結論.
解答 解:(1)方法一:如圖 ①,延長AC,DF相交于點M,
①,延長AC,DF相交于點M,
∵△ABC為等邊三角形,∴
AC=AB,∠BAC=60°,
∵∠BDE=120°,
∴DE∥AC,
∴∠M=∠EDF,
∵點F是CE中點,
∴CF=EF,
在△CFM和△EFD中,$\left\{\begin{array}{l}{∠M=∠EDF}\\{∠CFM=∠EFD}\\{CF=EF}\end{array}\right.$,
∴△CFM≌△EFD,
∴FM=FD,CM=DE,
∵BD=DE,
∴BD=CM.
∴AC+CM=AB+BD,
∴AM=AD,
∵FM=FD,
∴∠DAF=∠CAF=$\frac{1}{2}$∠BAC=30°,AF⊥DF,
∴AF=$\sqrt{3}$DF,
方法二,如圖, 連接BF,
連接BF,
∵∠BDE=120°,BD=DE,
∴∠DBE=30°,
∵∠ABC=60°,
∴∠CBE=90°,
∵點F是CE中點,
∴BF=EF=CF,
在△BDF和△EDF中,$\left\{\begin{array}{l}{BD=DE}\\{DF=DF}\\{BF=EF}\end{array}\right.$,
∴△BDF≌△EDF,
∴∠BFD=∠EFD,
同理:△ABF≌△ACF,
∴∠BAF=∠CAF=$\frac{1}{2}$∠BAC=30°,∠AFB=∠AFC,
∵∠AFD+∠AFC+∠EFD=180°,
∴∠AFD=90°,
在Rt△AFD中,∠DAF=30°,
∴AF=$\sqrt{3}$DF,
故答案為:AF⊥DF,AF=$\sqrt{3}$DF;
(2)(1)的結論仍然成立,
理由:如圖②, 延長DF至M使FM=FD,連接CM,AM,
延長DF至M使FM=FD,連接CM,AM,
∵點F是CE中點,
∴CF=EF,
在△MCF和△DEF中,$\left\{\begin{array}{l}{CF=EF}\\{∠CFM=∠EFD}\\{FM=FD}\end{array}\right.$,
∴△MCF≌△DEF,
∴CM=DE,
∵BD=DE,
∴CM=BD,
由旋轉知,∠CBD=60°,
∵BD=DE.∠BDE=120°,
∴∠BED=∠EBD=30°,
∴∠CBE=30°=∠BED,
∴DE∥BC,
∴∠BCE+∠CED=180°,
∵△MCF≌△DEF,
∴∠FCM=∠FED,
∴∠FCM+∠BCE=180°,
∴點M,C,B在同一條直線上,
∵∠ACB=60°,
∴∠ACM=120°
在△ACM和△ABD中,$\left\{\begin{array}{l}{AC=AB}\\{∠ACM=∠ABD=120°}\\{CM=BD}\end{array}\right.$,
∴△ACM≌△ABD,
∴∠CAM=∠BAD,AM=AD,
∵FM=FD,
∴AF⊥DF,
∵∠BAC=60°,
∴∠BAD+∠DAF+∠CAF=60°,
∴∠DAF+∠MAC+∠CAF=2∠DAF=60°,
∴∠DAF=30°,
∴AF=$\sqrt{3}$DF,
即:AF⊥DF,AF=$\sqrt{3}$DF,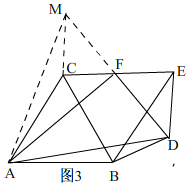
(3)(1)的結論仍然成立,
理由:如圖3,延長DF至M使FM=FD,連接CM,AM,
∵點F是CE中點,
∴CF=EF,
在△MCF和△DEF中,$\left\{\begin{array}{l}{CF=EF}\\{∠CFM=∠EFD}\\{FM=FD}\end{array}\right.$,
∴△MCF≌△DEF,
∴∠MCF=∠DEF,CM=DE,
∵BD=DE,
∴CM=BD,
∵∠ABD=∠ABC+∠CBE+∠DBE=90°+∠CBE,
∵∠ACM=360°-∠MCF-∠ACB-∠BCE
=360°-∠DEF-60°-∠BCE
=300°-∠DEF-∠BCE
=300°-(∠BED+∠BEC)-∠BCE
=300°-(30°+∠BEC)-∠BCE
=270°-(∠BCE+∠BEC)
=270°-(180°-∠CBE)
=90°+∠CBE,
∴∠ACM=∠ABD,
在△ACM和△ABD中,$\left\{\begin{array}{l}{AC=AB}\\{∠ACM=∠ABD}\\{CM=BD}\end{array}\right.$,
∴△ACM≌△ABD,
∴∠CAM=∠BAD,AM=AD,
∵FM=FD,
∴AF⊥DF,
∵∠BAC=60°,
∴∠BAD+∠DAF+∠CAF=60°
∴∠DAF+∠MAC+∠CAF=2∠DAF=60°,
∴∠DAF=30°,
∴AF=$\sqrt{3}$DF,
即:AF⊥DF,AF=$\sqrt{3}$DF.
點評 此題是幾何變換綜合題,主要考查了直角三角形斜邊的中線等于斜邊的一半,含30°的直角三角形的性質,等邊三角形的性質,全等三角形的判定和性質,周角的定義,垂直的方法的判定,利用倍長中線法構造全等三角形是解本題的關鍵,(3)判斷出∠ACM=∠ABD是解本題的難點,屬于中考壓軸題.


科目:初中數學 來源: 題型:選擇題
 將一列整數1,2,3,-4,-5,-6,7,-8,-9,-10,…按如圖所示排列.如第一個頂峰的數是-6,第二個峰頂的數是15,那么第2016個峰頂的數是( )
將一列整數1,2,3,-4,-5,-6,7,-8,-9,-10,…按如圖所示排列.如第一個頂峰的數是-6,第二個峰頂的數是15,那么第2016個峰頂的數是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{a+b}{2}$ | B. | $\frac{a+b}{11}$ | C. | $\frac{5a+6b}{11}$ | D. | $\frac{1}{2}$($\frac{a}{5}$+$\frac{b}{6}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
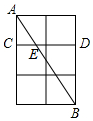 如圖,在2×3的方格紙中,每個小正方形的邊長均為1,點A,B,C,D都在格點上,AB與CD交于點E,則EB的長為$\frac{2\sqrt{13}}{3}$.
如圖,在2×3的方格紙中,每個小正方形的邊長均為1,點A,B,C,D都在格點上,AB與CD交于點E,則EB的長為$\frac{2\sqrt{13}}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 飛機上升9000米,再上升-5000米,則飛機實際上升4000米 | |
| B. | 一個正數,一個負數,它們表示的意義一定相反 | |
| C. | 0是最小的有理數 | |
| D. | 正數和負數統稱為有理數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com