等腰三角形ABC中，AB=AC，AD是角平分線，則“①AD⊥BC，②BD=DC，③∠B=∠C，④∠BAD=∠CAD”中，結論正確的個數是（ ）
A、4 B、3 C、2 D、1
科目：初中數學 來源：2014-2015學年江蘇省江陰市要塞片九年級上學期期中考試數學試卷（解析版） 題型：解答題
（本題6分）已知：如圖△ABC中，AC=BC，以BC為直徑的⊙O交AB于點D，過點D作DE⊥AC于E，交BC的延長線于點F．
求證：（1）AD=BD；
（2）DF是⊙O的切線.
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市八年級上學期期中考試數學試卷（解析版） 題型：填空題
把三邊分別為BC＝3，AC＝4，AB＝5的三角形沿最長邊AB翻折成
△ABC'，則CC'的長為
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市九年級上學期期中考試數學試卷（解析版） 題型：解答題
閱讀材料：（8分）
例：說明代數式 
的幾何意義，并求它的最小值．
【解析】
，如圖，建立平面直角坐標系，點P（x，0）是x軸上一點，則
可以看成點P與點A（0，1）的距離，
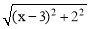可以看成點P與點B（3，2）的距離，所以原代數式的值可以看成線段PA與PB長度之和，它的最小值就是PA＋PB的最小值．
設點A關于x軸的對稱點為A′，則PA＝PA′，因此，求PA＋PB的最小值，只需求PA′＋PB的最小值，而點A′、B間的直線段距離最短，所以PA′＋PB的最小值為線段A′B的長度．為此，構造直角三角形A′CB，因為A′C＝3，CB＝3，所以A′B＝3
， 即原式的最小值為3．
根據以上閱讀材料，解答下列問題：
（1）代數式
的值可以看成平面直角坐標系中點P（x，0）與點A（1，1）、點B 的距離之和．（填寫點B的坐標）
（2）代數式 
的最小值.
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市九年級上學期期中考試數學試卷（解析版） 題型：選擇題
⊙A半徑為5，圓心A的坐標為（1，0），點P的坐標為（-2，4），則點P與⊙A的位置關系是（ ）
A．點P在⊙A上 B．點P在⊙A內
C．點P在⊙A外 D．點P在⊙A上或外
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市九年級上學期期中考試數學試卷（解析版） 題型：填空題
如圖，四邊形ABCD為圓內接四邊形，E為DA延長線上一點，若∠C＝50°,則∠BAE= º．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的算術平方根是 ；
的立方根是 ；
