
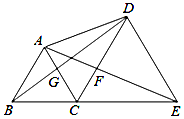
 如圖所示,點B、C、E在同一條直線上,AC=BC,CD=CE,∠ACB=∠DCE=60°.則下列結論:①△ACE≌△BCD;②CG=CF;③若連接GF,則GF∥BE;④△ADB≌△CEA.一定成立的有①②③.
如圖所示,點B、C、E在同一條直線上,AC=BC,CD=CE,∠ACB=∠DCE=60°.則下列結論:①△ACE≌△BCD;②CG=CF;③若連接GF,則GF∥BE;④△ADB≌△CEA.一定成立的有①②③. 分析 ①根據SAS證明△ACE≌△BCD;
②證△BCG≌△ACF可得結論;
③根據有一個角是60°的等腰三角形是等邊三角形,可得△GCF是等邊三角形,并由內錯角相等可得兩直線平行;
④因為AD不一定等于CD,所以△ADB≌△CEA不一定成立.
解答 解:①∵∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{EC=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS);
故①正確;
②∵△ACE≌△BCD,
∴∠CAF=∠CBG,
∵∠ACB=∠DCE=60°,
∴∠ACD=60°,
∴∠ACB=∠ACF=60°,
在△BCG和△ACF中,
∵$\left\{\begin{array}{l}{∠CAF=∠CBG}\\{AC=BC}\\{∠ACB=∠ACF}\end{array}\right.$,
∴△BCG≌△ACF(ASA),
∴CG=CF;
故②正確;
③∵CG=CF,∠ACF=60°,
∴△GCF是等邊三角形,
∴∠CGF=60°,
∴∠CGF=∠BCG=60°,
∴GF∥BE,
故③正確;
④因為AD不一定等于CD,由已知條件無法得到△ADB≌△CEA;
所以本題一定成立的有:①②③;
故答案為:①②③.
點評 本題考查了全等三角形的性質和判定,解答此題的關鍵是找到可證三角形全等的條件即可.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 兩直角邊對應相等 | B. | 斜邊和一條直角邊對應相等 | ||
| C. | 兩銳角對應相等 | D. | 一個銳角和斜邊對應相等 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 蘋果品種 | A | B | C |
| 每輛汽車裝載量/噸 | 2.2 | 2.1 | 2 |
| 每噸蘋果獲利/元 | 600 | 800 | 500 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 不變 | B. | 擴大3倍 | C. | 縮小3倍 | D. | 縮小6倍 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com