
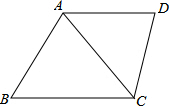
 如圖,梯形ABCD中,AD∥BC,AC為對角線,且∠DCA=∠B,線段AD、BC的長是方程x(x-4)+2(4-x)=0的兩根,且AD<BC,CD=3,求AB與AC的長.
如圖,梯形ABCD中,AD∥BC,AC為對角線,且∠DCA=∠B,線段AD、BC的長是方程x(x-4)+2(4-x)=0的兩根,且AD<BC,CD=3,求AB與AC的長. 分析 首先解方程求得AD和BC的長,然后得到△ABC∽△DCA,根據相似三角形對應邊的比相等列式計算即可.
解答 解:∵線段AD、BC的長是方程x(x-4)+2(4-x)=0的兩根,且AD<BC,
∴AD=2,BC=4,
∵AD∥BC,
∴∠DAC=∠BCA,
∵∠DCA=∠B,
∴△ABC∽△DCA,
∴$\frac{AB}{DC}=\frac{AC}{AD}=\frac{BC}{AC}$,
即:$\frac{AB}{3}=\frac{AC}{2}=\frac{4}{AC}$,
解得:AB=3$\sqrt{2}$,AC=2$\sqrt{2}$.
點評 本題考查了相似三角形的判定與性質、解一元二次方程及梯形的知識,解題的關鍵是能夠得到相似三角形,并正確的確定對應邊,難度不大.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:解答題
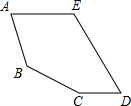 聰聰用五根寬度相同的木條拼成了一個五邊形,如圖所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.
聰聰用五根寬度相同的木條拼成了一個五邊形,如圖所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,將△ABC沿著過AB中點D的直線折疊,使點A落在BC邊上的A1處,稱為第1次操作,折痕DE到BC的距離記為h1,還原紙片后,再將△ADE沿著過AD中點D1的直線折疊,使點A落在DE邊上的A2處,稱為第2次操作,折痕D1E1到BC的距離記為h2;按上述方法不斷操作下去…,經過第2015次操作后得到的折痕D2014E2014,到BC的距離記為h2015;若h1=1,則h2016的值為2-$\frac{1}{{2}^{2015}}$.
如圖,將△ABC沿著過AB中點D的直線折疊,使點A落在BC邊上的A1處,稱為第1次操作,折痕DE到BC的距離記為h1,還原紙片后,再將△ADE沿著過AD中點D1的直線折疊,使點A落在DE邊上的A2處,稱為第2次操作,折痕D1E1到BC的距離記為h2;按上述方法不斷操作下去…,經過第2015次操作后得到的折痕D2014E2014,到BC的距離記為h2015;若h1=1,則h2016的值為2-$\frac{1}{{2}^{2015}}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
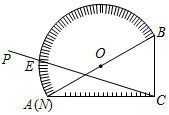 如圖,量角器的直徑與直角三角板ABC的斜邊AB重合,其中量角器0刻度線的端點N與點A重合,射線CP從CA處出發沿順時針方向以每秒2度的速度旋轉,CP與量角器的半圓弧交于點E,第23秒時,點E在量角器上對應的度數是92度.
如圖,量角器的直徑與直角三角板ABC的斜邊AB重合,其中量角器0刻度線的端點N與點A重合,射線CP從CA處出發沿順時針方向以每秒2度的速度旋轉,CP與量角器的半圓弧交于點E,第23秒時,點E在量角器上對應的度數是92度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com